
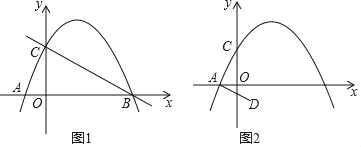
【題目】已知:拋物線y=﹣![]() x2+bx+c交x軸于點A(﹣1,0)和點B,交y軸于點C(0,2)
x2+bx+c交x軸于點A(﹣1,0)和點B,交y軸于點C(0,2)
(1)求拋物線的表達式;
(2)點P為第一象限拋物線上一點,是否存在使△PBC面積最大的點P?若不存在,請說明理由;若存在,求出點P的坐標;
(3)點D坐標為(1,﹣1),連接AD,將線段AD繞平面內某一點旋轉180度得線段MN(點M、N分別與點A、D對應),使點M、N都在拋物線上,求點M、N的坐標.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)當x=2時,S有最大值為4,此時P(2,3);(3)N(1,3),M(3,2).
x+2;(2)當x=2時,S有最大值為4,此時P(2,3);(3)N(1,3),M(3,2).
【解析】
(1) 根據拋物線y=y=﹣![]() x2+bx+c經過A (-1, 0)C(0,2)兩點,列出b和c的二元一次方程組,求出b和c的值, 進而求出拋物線的表達式;
x2+bx+c經過A (-1, 0)C(0,2)兩點,列出b和c的二元一次方程組,求出b和c的值, 進而求出拋物線的表達式;
(2)過點P作PQ//y軸,交直線BC于Q,設P(x,![]() ),則Q(x,
),則Q(x,![]() );求出PQ的長, 利用
);求出PQ的長, 利用![]() =
=![]() PQ.OB列出S關于的二次函數, 利用函數的性質求出面積的最大值,進而求出點P的坐標;
PQ.OB列出S關于的二次函數, 利用函數的性質求出面積的最大值,進而求出點P的坐標;
(3)作輔助線,根據線段AD繞平面內某一點旋轉180度得線段MN可知: 旋轉后的MN與AD平行且相等,構建全等三角形:ΔADG≌ΔMNG,根據A、 D兩點的坐標發現, N點向下平移1個單位再向右移動兩個單位得M,設N的坐標為:設N(m,![]() ) , 根據平移規律表示M (m+2,
) , 根據平移規律表示M (m+2, ![]() ) , 代入拋物線的解析式即可
) , 代入拋物線的解析式即可
(1)∵拋物線y=﹣![]() x2+bx+c交x軸于點A(﹣1,0)和點B,交y軸于點C(0,2),
x2+bx+c交x軸于點A(﹣1,0)和點B,交y軸于點C(0,2),
∴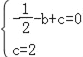 ,
,
解得![]() ,
,
∴拋物線的解析式:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵令y=0,則=﹣![]() x2+
x2+![]() x+2=0,
x+2=0,
解得x1=﹣1,x2=4
∴B(4,0),
∴直線BC:y=﹣![]() x+2;
x+2;
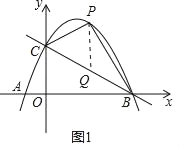
如圖1,過點P作PQ∥y軸,交直線BC于Q,
設P(x,﹣![]() x2+
x2+![]() x+2),則Q(x,﹣
x+2),則Q(x,﹣![]() x+2);
x+2);
∴PQ=(﹣![]() x2+
x2+![]() x+2)﹣(﹣
x+2)﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x2+2x,
x2+2x,
S△PCB=![]() PQOB=
PQOB=![]() ×(﹣
×(﹣![]() x2+2x)×4=﹣(x﹣2)2+4;
x2+2x)×4=﹣(x﹣2)2+4;
當x=2時,S有最大值為4,此時P(2,3);
(3)如圖2,過D作DG⊥x軸于G,過N作NH∥y軸,過M作MH∥x軸,交于H,

由題意得:△ADG≌△MNG,
∵A(﹣1,0),D(1,﹣1),
∴AG=2,DG=1,
∴NH=DG=1,MH=AG=2,
設N(m,﹣![]() m2+
m2+![]() m+2),則M(m+2,﹣
m+2),則M(m+2,﹣![]() m2+
m2+![]() m+2﹣1),
m+2﹣1),
把M的坐標代入拋物線y=﹣![]() x2+
x2+![]() x+2中得:
x+2中得:
﹣![]() (m+2)2+
(m+2)2+![]() (m+2)+2=﹣
(m+2)+2=﹣![]() m2+
m2+![]() m+2﹣1,
m+2﹣1,
解得:m=1,
當m=1時,﹣![]() m2+
m2+![]() m+2=3,
m+2=3,
∴N(1,3),M(3,2).


科目:初中數學 來源: 題型:
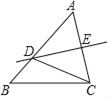
【題目】如圖,在△ABC中,AB=5,AC=4,∠A=60°,若邊AC的垂直平分線DE交AB于點D,連接CD,則△BDC的周長為( )
A. 8 B. 9 C. 5+![]() D. 5+
D. 5+![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知 AB 是⊙O 的直徑,點 C、D 在⊙O 上,過 D 點作 PF∥AC交⊙O 于 F,交 AB 于點 E,∠BPF=∠ADC
(1)求證:AEEB=DEEF.
(2)求證:BP 是⊙O 的切線:
(3)當的半徑為![]() ,AC=2,BE=1 時,求 BP 的長,
,AC=2,BE=1 時,求 BP 的長,

查看答案和解析>>
科目:初中數學 來源: 題型:
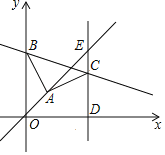
【題目】如圖,平面直角坐標系中,![]() ,
,![]() 為
為![]() 軸正半軸上一點,連接
軸正半軸上一點,連接![]() ,在第一象限作
,在第一象限作![]() ,
,![]() ,過點
,過點![]() 作直線
作直線![]() 軸于
軸于![]() ,直線
,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,且
,且![]() ,則直線
,則直線![]() 解析式為____________.
解析式為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列命題:①在直角三角形ABC中,已知兩邊長為3和4,則第三邊長為5;②三角形的三邊a、b、c滿足a2+c2=b2,則∠C=90°;③△ABC中,若∠A:∠B:∠C=1:5:6,則△ABC是直角三角形;④△ABC中,若a:b:c=1:2:![]() ,則這個三角形是直角三角形,其中,正確命題為_____(選填序號).
,則這個三角形是直角三角形,其中,正確命題為_____(選填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點D是AC的中點.將一塊銳角為45°的直角三角板如圖放置,使三角板斜邊的兩個端點分別與A、D重合,連接BE、EC.
 試猜想線段BE和EC的數量及位置關系,并證明你的猜想.
試猜想線段BE和EC的數量及位置關系,并證明你的猜想.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AC=BC,點D是BC上一點,∠ADE=∠C.
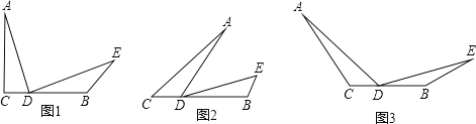
(1)如圖1,若∠C=90°,∠DBE=135°.
①求證:∠EDB=∠CAD;
②求證:DA=DE;
(2)如圖2,若∠C=40°,DA=DE,求∠DBE的度數;
(3)如圖3,請直接寫出∠DBE與∠C之間滿足什么數量關系時,總有DA=DE成立.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】□ABCD中,E、F是對角線BD上不同的兩點,下列條件中,不能得出四邊形AECF一定為平行四邊形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com