
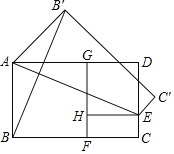
【題目】如圖,在黃金矩形ABCD中,四邊形ABFG、GHED均為正方形,![]() ,現將矩形ABCD沿AE向上翻折,得四邊形AEC'B',連接BB',若AB=2,則線段BB'的長度為( )
,現將矩形ABCD沿AE向上翻折,得四邊形AEC'B',連接BB',若AB=2,則線段BB'的長度為( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
【答案】A
【解析】
BB′交AE于M,作EH⊥AB′于H,連接B′E,如圖,利用黃金矩形的定義得到BC=![]() +1,再利用正方形的性質得到AG=AB=2,DE=DG=
+1,再利用正方形的性質得到AG=AB=2,DE=DG=![]() ﹣1,則利用勾股定理得到AE=2
﹣1,則利用勾股定理得到AE=2![]() ,接著利用折疊的性質得到C′B′=CB=
,接著利用折疊的性質得到C′B′=CB=![]() +1,EC′=EC=3﹣
+1,EC′=EC=3﹣![]() ,AB′=AB=2,BB′⊥AE,B′M=BM,則EH=C′B′=
,AB′=AB=2,BB′⊥AE,B′M=BM,則EH=C′B′=![]() +1,然后利用面積法求出B′M,從而得到BB′的長.
+1,然后利用面積法求出B′M,從而得到BB′的長.
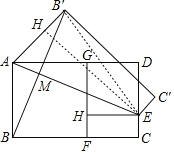
解:BB′交AE于M,作EH⊥AB′于H,連接B′E,如圖,
∵四邊形ABCD為黃金矩形,
∴AB=![]() BC,
BC,
∴BC=![]() ×2=
×2=![]() +1,
+1,
∵四邊形ABFG、GHED均為正方形,
∴AG=AB=2,DE=DG=![]() +1﹣2=
+1﹣2=![]() ﹣1,
﹣1,
在Rt△ADE中,AE=![]() =2
=2![]() ,
,
∵矩形ABCD沿AE向上翻折,得四邊形AEC'B',
∴C′B′=CB=![]() +1,EC′=EC=3﹣
+1,EC′=EC=3﹣![]() ,AB′=AB=2,BB′⊥AE,B′M=BM,
,AB′=AB=2,BB′⊥AE,B′M=BM,
易得四邊形B′C′EH為矩形,則EH=C′B′=![]() +1,
+1,
∵![]() B′M×AE=
B′M×AE=![]() AB′×EH,
AB′×EH,
∴B′M=![]() =
=![]() ,
,
∴BB′=2B′M=![]() .
.
故選:A.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,當m,n滿足mn=k(k為常數,且m>0,n>0)時,就稱點(m,n)為“等積點”.若直線y=﹣x+b(b>0)與x軸、y軸分別交于點A和點B,并且該直線上有且只有一個“等積點”,過點A與y軸平行的直線和過點B與x軸平行的直線交于點C,點E是直線AC上的“等積點”,點F是直線BC上的“等積點”,若△OEF的面積為![]() ,則OE=______.
,則OE=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△ABC的邊長是2,D、E分別為AB、AC的中點,延長BC至點F,使CF=![]() BC,連接CD和EF.
BC,連接CD和EF.

(1)求證:DE=CF;
(2)求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
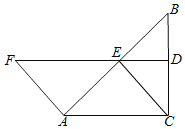
【題目】如圖,在△ABC中,∠ACB=90°,BC的垂直平分線DE交BC于D,交AB于E,點F在DE的延長線上,且AF=CE=AE.
(1)求證:四邊形ACEF是平行四邊形;
(2)當∠B=30°時,試猜想四邊形ACEF是什么圖形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水產品養殖企業為指導該企業某種產品的養殖和銷售,對歷年市場行情和水產品的養殖情況進行了調查.調查發現這種水產品的每千克售價![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足關系式
(月)滿足關系式![]() +36,而其每千克成本
+36,而其每千克成本![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足的函數關系如圖所示:
(月)滿足的函數關系如圖所示:
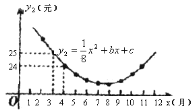
(1)試確定![]() 、
、![]() 的值;
的值;
(2)求出這種水產品每千克的利潤![]() (元)與銷售月份
(元)與銷售月份![]() (月)之間的函數關系式;
(月)之間的函數關系式;
(3)幾月份出售這種水產品每千克利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個四位數,若首位和末位都是1,稱這樣的數為“首尾雙一數”,例如:1231,1581,1941等都是“首尾雙一數”.
(1)證明:一個“首尾雙一數”與它去掉首位和末位后得到的兩位數的3倍的差能被7整除;
(2)給定一個“首尾雙一數”n,記D(n)=![]() ,求滿足D(n)是完全平方數,且n的所有位數上的數字之和為偶數的所有n.
,求滿足D(n)是完全平方數,且n的所有位數上的數字之和為偶數的所有n.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司共有![]() 三個部門,根據每個部門的員工人數和相應每人所創的年利潤繪制成如下的統計表和扇形圖.
三個部門,根據每個部門的員工人數和相應每人所創的年利潤繪制成如下的統計表和扇形圖.

各部門人數及每人所創年利潤統計表
部門 | 員工人數 | 每人所創的年利潤/萬元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形圖中,C部門所對應的圓心角的度數為___________;
②在統計表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求這個公司平均每人所創年利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com