
【題目】某市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧工作,幫助農民組建農副產品銷售公司,某農副產品的年產量不超過100萬件,該產品的生產費用y(萬元)與年產量x(萬件)之間的函數圖象是頂點為原點的拋物線的一部分(如圖①所示);該產品的銷售單價z(元/件)與年銷售量x(萬件)之間的函數圖象是如圖②所示的一條線段,生產出的產品都能在當年銷售完,達到產銷平衡,所獲毛利潤為w萬元.(毛利潤=銷售額﹣生產費用)

(1)請直接寫出y與x以及z與x之間的函數關系式;
(2)求w與x之間的函數關系式;并求年產量多少萬件時,所獲毛利潤最大?最大毛利潤是多少?
(3)由于受資金的影響,今年投入生產的費用不會超過360萬元,今年最多可獲得多少萬元的毛利潤?
【答案】(1)y=![]() x2,z=﹣
x2,z=﹣![]() x+30;(2)W==﹣
x+30;(2)W==﹣![]() x2+30x,年產量為75萬件時毛利潤最大,最大毛利潤為1125萬元;(3)今年最多可獲得1080萬元的毛利潤.
x2+30x,年產量為75萬件時毛利潤最大,最大毛利潤為1125萬元;(3)今年最多可獲得1080萬元的毛利潤.
【解析】
(1)結合圖象,利用待定系數法求出y與x以及z與x之間的函數關系式即可;(2)根據毛利潤=銷售額﹣生產費用可得w與x之間的函數關系式,再利用二次函數的性質求解即可;(3)令y=0,解方程求得x的值,根據圖象結合y的取值范圍,求得x的取值范圍,再由二次函數的性質即可解答.
(1)圖①可得函數經過點(100,1000),
設拋物線的解析式為y=ax2(a≠0),
將點(100,1000)代入得:1000=10000a,
解得:a=![]() ,
,
故y與x之間的關系式為y=![]() x2.
x2.
圖②可得:函數經過點(0,30)、(100,20),
設z=kx+b,則![]() ,
,
解得: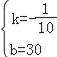 ,
,
故z與x之間的關系式為z=﹣![]() x+30;
x+30;
(2)W=zx﹣y=﹣![]() x2+30x﹣
x2+30x﹣![]() x2
x2
=﹣![]() x2+30x
x2+30x
=﹣![]() (x2﹣150x)
(x2﹣150x)
=﹣![]() (x﹣75)2+1125,
(x﹣75)2+1125,
∵﹣![]() <0,
<0,
∴當x=75時,W有最大值1125,
∴年產量為75萬件時毛利潤最大,最大毛利潤為1125萬元;
(3)令y=360,得![]() x2=360,
x2=360,
解得:x=±60(負值舍去),
由圖象可知,當0<y≤360時,0<x≤60,
由W=﹣![]() (x﹣75)2+1125的性質可知,
(x﹣75)2+1125的性質可知,
當0<x≤60時,W隨x的增大而增大,
故當x=60時,W有最大值1080,
答:今年最多可獲得毛利潤1080萬元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
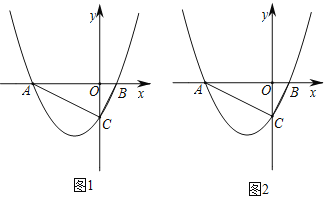
【題目】已知,拋物線y=![]() m與y軸交于點C,與x軸交于點A和點B(其中點A在y軸左側,點B在y軸右側).
m與y軸交于點C,與x軸交于點A和點B(其中點A在y軸左側,點B在y軸右側).
(1)若拋物線y=![]() m的對稱軸為直線x=1,求拋物線的解析式;
m的對稱軸為直線x=1,求拋物線的解析式;
(2)如圖1,∠ACB=90°,點P是拋物線y=![]() m上的一點,若S△BCP=
m上的一點,若S△BCP=![]() ,求點P的坐標;
,求點P的坐標;
(3)如圖2,過點A作AD∥BC交拋物線于點D,若點D的縱坐標為﹣![]() m,求直線AD的解析式.
m,求直線AD的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系![]() 中的點
中的點![]() 和圖形
和圖形![]() ,給出如下定義:若圖形
,給出如下定義:若圖形![]() 上存在兩個點
上存在兩個點![]() ,使得
,使得![]() 是邊長為2的等邊三角形,則稱點
是邊長為2的等邊三角形,則稱點![]() 是圖形
是圖形![]() 的一個“和諧點”.
的一個“和諧點”.
已知直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() 的半徑為
的半徑為![]() .
.
(1)若![]() ,在點
,在點![]() 中,直線
中,直線![]() 的和諧點是___________;
的和諧點是___________;
(2)若![]() 上恰好存在2個直線
上恰好存在2個直線![]() 的和諧點,求
的和諧點,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,線段
,線段![]() 上存在
上存在![]() 的和諧點,直接寫出
的和諧點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:正方形ABCD中,∠MAN=45°,∠MAN繞點A順時針旋轉,它的兩邊分別交CB、DC(或它們的延長線)于點M、N.
(1)當∠MAN繞點A旋轉到BM=DN時(如圖1),請你直接寫出BM、DN和MN的數量關系:__________.
(2)當∠MAN繞點A旋轉到BM≠DN時(如圖2),(1)中的結論是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明.
(3)當∠MAN繞點A旋轉到如圖3的位置時,線段BM、DN和MN之間又有怎樣的數量關系?請寫出直接寫出結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對垃圾進行分類投放,能提高垃圾處理和再利用的效率,減少污染,保護環境.為了檢查垃圾分類的落實情況,某居委會成立了甲、乙兩個檢查組,采取隨機抽查的方式分別對轄區內的A,B,C,D四個小區進行檢查,并且每個小區不重復檢查.
(1)甲組抽到A小區的概率是多少;
(2)請用列表或畫樹狀圖的方法求甲組抽到A小區,同時乙組抽到C小區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
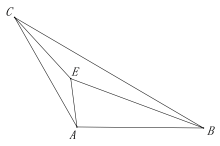
【題目】如圖,在△ABC中,∠CAB=120°,AB=AC=3,點E是三角形ABC 內一點,且滿足![]() 則點E 在運動過程中所形成的圖形的長為 ( )
則點E 在運動過程中所形成的圖形的長為 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】廣州融創樂園是國內首個以南越文化、嶺南風格為主題的游樂園,自2019年6月開園以來受到了國內外游客的熱捧.某旅游團組織一批游客游玩了樂園內的四個網紅項目,“A.雙龍飛舞”、“B.飛躍廣東”、“C.云霄塔”、“D.怒海狂濤”,并進行了“我最喜歡的一個項目”的投票評選活動,投票結果繪制成以下兩幅尚未完整的統計圖.請你根據圖中提供的信息,解答下列問題:
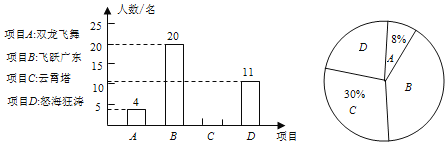
(1)參與投票的游客總人數為 人;
(2)扇形統計圖中B所對的圓心角度數為 度,并補全條形統計圖;
(3)從投票給“雙龍飛舞“的3名男生和1名女生中隨機抽取2名了解情況,請你用列舉法求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點C為線段![]() 上一點,以
上一點,以![]() 為斜邊作等腰
為斜邊作等腰![]() ,連接
,連接![]() ,在
,在![]() 外側,以
外側,以![]() 為斜邊作等腰
為斜邊作等腰![]() ,連接
,連接![]() .
.
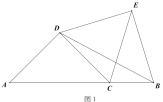
(1)如圖1,當![]() 時:
時:
①求證:![]() ;
;
②判斷線段![]() 與
與![]() 的數量關系,并證明;
的數量關系,并證明;
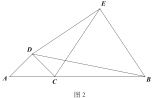
(2)如圖2,當![]() 時,
時,![]() 與
與![]() 的數量關系是否保持不變?
的數量關系是否保持不變?
對于以上問題,小牧同學通過觀察、實驗,形成了解決該問題的幾種思路:
想法1:嘗試將點D為旋轉中心,過點D作線段![]() 垂線,交
垂線,交![]() 延長線于點G,連接
延長線于點G,連接![]() ;通過證明
;通過證明![]() 解決以上問題;
解決以上問題;
想法2:嘗試將點D為旋轉中心,過點D作線段![]() 垂線,垂足為點G,連接
垂線,垂足為點G,連接![]() .通過證明
.通過證明![]() 解決以上問題;
解決以上問題;
想法3:嘗試利用四點共圓,過點D作![]() 垂線段
垂線段![]() ,連接
,連接![]() ,通過證明D、F、B、E四點共圓,利用圓的相關知識解決以上問題.
,通過證明D、F、B、E四點共圓,利用圓的相關知識解決以上問題.
請你參考上面的想法,證明![]() (一種方法即可).
(一種方法即可).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com