
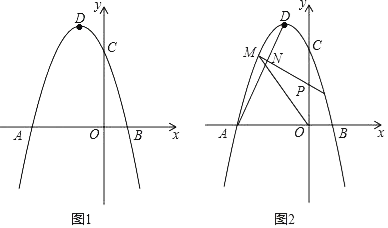
【題目】如圖,拋物線的頂點D的坐標為(﹣1,4),拋物線與x軸相交于A.B兩點(A在B的左側),與y軸交于點C(0,3).
(1)求拋物線的表達式;
(2)如圖1,已知點E(0,﹣3),在拋物線的對稱軸上是否存在一點F,使得△CEF的周長最小,如果存在,求出點F的坐標;如果不存在,請說明理由;
(3)如圖2,連接AD,若點P是線段OC上的一動點,過點P作線段AD的垂線,在第二象限分別與拋物線、線段AD相交于點M、N,當MN最大時,求△POM的面積.
【答案】(1)y=﹣x2﹣2x+3;(2) 存在, F(﹣1,0),理由見解析;(3)2
【解析】
(1)根據頂點式可求得拋物線的表達式;
(2) 如圖 1,作 C關于對稱軸的對稱點 C′,連接EC′交對稱軸于 F,根據軸對稱的最短路徑問題, CF+EF的值最小,則△CEF的周長最小;
(3)如圖2,先利用待定系數法求AD的解析式為: y=2x+6,設M(m,﹣m2﹣2m+3),則G(m,2m+6),(﹣3≤m≤﹣1),證明△MNG∽△AHD,列比例式可得MN的表達式,根據配方法可得當m=-2時,MN有最大值,證明△MCP∽△DHA,同理得PC的長,從而得OP的長,根據三角形的面積公式可得結論,并將m=-2代入計算即可
(1)設拋物線的表達式為:y=a(x+1)2+4,
把x=0,y=3代入得:3=a(0+1)2+4,解得:a=﹣1
∴拋物線的表達式為y=﹣(x+1)2+4=﹣x2﹣2x+3;
(2)存在.如圖 1,作 C關于對稱軸的對稱點 C′,連接EC′交對稱軸于 F,此時 CF+EF的值最小,則△CEF的周長最小.
∵C(0,3),
∴C′(﹣2,3),易得C′E的解析式為:y=﹣3x﹣3,
當x=﹣1時,y=﹣3×(﹣1)﹣3=0,
∴F(﹣1,0)
(3)如圖2,∵A(﹣3,0),D(﹣1,4),
易得AD的解析式為:y=2x+6,
過點D作DH⊥x軸于H,過點M作MG⊥x軸交AD于G,
AH=﹣1﹣(﹣3)=2,DH=4,∴AD=![]() ,
,
設M(m,﹣m2﹣2m+3),則G(m,2m+6),(﹣3≤m≤﹣1),
∴MG=(﹣m2﹣2m+3)﹣(2m+6)=﹣m2﹣4m﹣3,
由題易知△MNG∽△AHD,
∴![]()
即![]()
∵![]()
∴當m=﹣2時,MN有最大值;
此時M(﹣2,3),又∵C(0,3),連接MC
∴MC⊥y軸
∵∠CPM=∠HAD,∠MCP=∠DHA=90°,
∴△MCP∽△DHA,
∴![]()
即 ![]()
∴PC=1
∴OP=OC﹣PG=3﹣1=2,
∴S△POM=![]() =2,
=2,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】 如圖,在Rt△ABC中,∠C=90°,點O在邊BC上,以點O為圓心,OB為半徑的圓經過點A,過點A作直線AD,使∠CAD=2∠B.

(1)判斷直線AD與⊙O的位置關系,并說明理由;
(2)若OB=4,∠CAD=60°,請直接寫出圖中弦AB與![]() 圍成的陰影部分的面積.
圍成的陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖1,已知水龍頭噴水的初始速度v0可以分解為橫向初始速度vx和縱向初始速度vy,θ是水龍頭的仰角,且v02=vx2+vy2.圖2是一個建在斜坡上的花圃場地的截面示意圖,水龍頭的噴射點A在山坡的坡頂上(噴射點離地面高度忽略不計),坡頂的鉛直高度OA為15米,山坡的坡比為![]() .離開水龍頭后的水(看成點)獲得初始速度v0米/秒后的運動路徑可以看作是拋物線,點M是運動過程中的某一位置.忽略空氣阻力,實驗表明:M與A的高度之差d(米)與噴出時間t(秒)的關系為d=vyt-5t2;M與A的水平距離為vxt米.已知該水流的初始速度v0為15米/秒,水龍頭的仰角θ為53°.
.離開水龍頭后的水(看成點)獲得初始速度v0米/秒后的運動路徑可以看作是拋物線,點M是運動過程中的某一位置.忽略空氣阻力,實驗表明:M與A的高度之差d(米)與噴出時間t(秒)的關系為d=vyt-5t2;M與A的水平距離為vxt米.已知該水流的初始速度v0為15米/秒,水龍頭的仰角θ為53°.

(1)求水流的橫向初始速度vx和縱向初始速度vy;
(2)用含t的代數式表示點M的橫坐標x和縱坐標y,并求y與x的關系式(不寫x的取值范圍);
(3)水流在山坡上的落點C離噴射點A的水平距離是多少米?若要使水流恰好噴射到坡腳B處的小樹,在相同仰角下,則需要把噴射點A沿坡面AB方向移動多少米?(參考數據:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
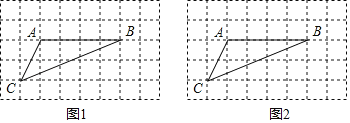
【題目】如圖,在8×5的正方形網格中,每個小正方形的邊長均為1,△ABC的三個頂點均在小正方形的頂點上.
(1)在圖1中畫出△ABD(點D在小正方形的頂點上),使△ABD的周長等于△ABC的周長,且四邊形ACBD是中心對稱圖形;
(2)在圖2中找一點E(點E在小正方形的頂點上),使tan∠AEB=2(AE<EB),且四邊形ACEB的對邊不平行,并直接寫出圖2中四邊形ACEB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
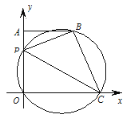
【題目】如圖,在平面直角坐標系中,A(0,4),B(3,4),P 為線段 OA 上一動點,過 O,P,B 三點的圓交 x 軸正半軸于點 C,連結 AB, PC,BC,設 OP=m.
(1)求證:當 P 與 A 重合時,四邊形 POCB 是矩形.
(2)連結 PB,求 tan∠BPC 的值.
(3)記該圓的圓心為 M,連結 OM,BM,當四邊形 POMB 中有一組對邊平行時,求所有滿足條件的 m 的值.
(4)作點 O 關于 PC 的對稱點O ,在點 P 的整個運動過程中,當點O 落在△APB 的內部 (含邊界)時,請寫出 m 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“2018西安國際馬拉松”于2018年10月20日在陜西西安舉行,該賽事共有三項:![]() .“馬拉松”、
.“馬拉松”、![]() .“半程馬拉松”、
.“半程馬拉松”、![]() .“迷你馬拉松”小明和小剛有幸參與了該項賽事的志愿者服務工作,組委會隨機將志愿者分配到三個項目組.
.“迷你馬拉松”小明和小剛有幸參與了該項賽事的志愿者服務工作,組委會隨機將志愿者分配到三個項目組.
(1)小明被分配到“迷你馬拉松”項目組的概率為________.
(2)利用列表或樹狀圖求小明和小剛被分配到不同項目組的概率________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小峰和小軒用兩枚質地均勻的骰子做游戲,規則如下:每人隨機擲兩枚骰子一次(若擲出的兩枚骰子摞在一起,則重擲),點數和大的獲勝;點數和相同為平局.
依據上述規則,解答下列問題:
(1)隨機擲兩枚骰子一次,用列表法或樹狀圖法求點數和為10的概率;
(2)小峰先隨機擲兩枚骰子一次,點數和是10,求小軒隨機擲兩枚骰子一次,勝小峰的概率.(骰子:六個面分別有1、2、3、4、5、6個小圓點的立方塊.點數和:兩枚骰子朝上的點數之和.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲口袋中裝有兩個相同的小球,它們分別寫有1和2;乙口袋中裝有三個相同的小球,它們分別寫有3、4和5;丙口袋中裝有兩個相同的小球,它們分別寫有6和7.從這3個口袋中各隨機地取出1個小球.
(1)取出的3個小球上恰好有兩個偶數的概率是多少?
(2)取出的3個小球上全是奇數的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于以AB為直徑的⊙O,過點A作⊙O的切線,與BC的延長線相交于點D,在CB上截取CE=CD,連接AE并延長,交⊙O于點F,連接CF.
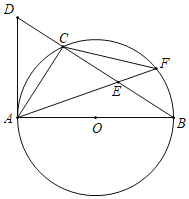
(1)求證:AC=CF;
(2)若AB=4,sinB![]() ,求EF的長.
,求EF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com