【題目】如果事件A發生的概率是 
，那么在相同條件下重復試驗，下列4種陳述中，不正確的有 ①說明做100次這種試驗，事件A必發生1次
②說明事件A發生的頻率是
③說明做100次這種試驗中，前99次事件A沒發生，后1次事件A才發生
④說明做100次這種試驗，事件A可能發生1次（ ）
A.①、②、③
B.①、②、④
C.②、③、④
D.①、②、③、④
【答案】A
【解析】解：∵事件A發生的概率是 
，并不能說明做100次這種試驗，事件A必發生1次，有可能多次，也有可能1次不發生， ∴選項①符合題意；
∵事件A發生的概率是 ，并不能說明事件A發生的頻率是 ，
∴選項②符合題意；
∵事件A發生的概率是 ，并不能說明做100次這種試驗中，前99次事件A沒發生，后1次事件A才發生，
∴選項③符合題意；
∵事件A發生的概率是 ，說明做100次這種試驗，事件A可能發生1次，
∴選項④不符合題意，
∴4種陳述中，不正確的有：①、②、③．
故選：A．
【考點精析】利用概率的意義對題目進行判斷即可得到答案，需要熟知任何事件的概率是0~1之間的一個確定的數，它度量該事情發生的可能性．小概率事件很少發生，而大概率事件則經常發生．知道隨機事件的概率有利于我們作出正確的決策．
世紀百通期末金卷系列答案科目：初中數學 來源： 題型：
【題目】為了減少霧霾，美化環境，小王上班的交通方式由駕車改為騎自行車，小王家距單位的路程是15千米，在相同的路線上，小王駕車的速度是騎自行車速度的4倍，小王每天騎自行車上班比駕車上班要早出發45分鐘，才能按原時間到達單位，求小王騎自行車的速度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】請仔細閱讀下面材料，然后解決問題：
在分式中，對于只含有一個字母的分式，當分子的次數大于或等于分母的次數時，我們稱之為“假分式”．例如： 
， 
；當分子的次數小于分母的次數時，我們稱之為“真分式”，例如： 
， 
．我們知道，假分數可以化為帶分數，例如： 
，類似的，假分式也可以化為“帶分式”（整式與真分式和的形式），例如： 
．
（1）將分式
化為帶分式；
（2）當x取哪些整數值時，分式
的值也是整數？
（3）當x的值變化時，分式
的最大值為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一次函數y=x+b，它的圖象與兩坐標軸所圍成的圖形的面積等于2．
（1）求b的值；
（2）若函數y=x+b的圖象交y軸于正半軸，則當x取何值時，y的值是正數？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某手機經銷商計劃同時購進一批甲、乙兩種型號手機，若購進2部甲型號手機和5部乙型號手機，共需資金6000元；若購進3部甲型號手機和2部乙型號手機，共需資金4600元．
（1）求甲、乙型號手機每部進價多少元？
（2）為了提高利潤，該店計劃購進甲、乙型號手機銷售，預計用不多于1.8萬元且不少于1.76萬元的資金購進這兩種手機共20部，請問有幾種進貨方案？
（3）若甲型號手機的售價為1500元，乙型號手機的售價為1400元，為了促銷，公司決定每售出一部乙型號手機，返還顧客現金a元；而甲型號手機售價不變，要使（2）中所有方案獲利相同，求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】十八世紀瑞士數學家歐拉證明了簡單多面體中頂點數（V）、面數（F）、棱數（E）之間存在的一個有趣的關系式，請你觀察下列幾種簡單多面體模型，解答下列問題：
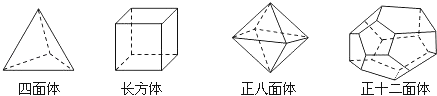
圖1 圖2
（探索新知）如圖1，（1）根據上面多面體模型，完成表格中的空格；
多面體 | 頂點數（V） | 面數（F） | 棱數（E） |
四面體 | 4 | 4 | |
長方體 | 8 | 6 | 12 |
正八面體 | 8 | 12 | |
正十二面體 | 20 | 12 | 30 |
你發現頂點數（V）、面數（F）、棱數（E）之間存在的關系式是 ．
（2）根據以上關系式猜想是否存在一個多面體，它有16個面，50條棱，34個頂點？并寫出理由。
（實際應用）如圖2，足球一般有32塊黑白皮子縫合而成，黑色的是正五邊形，白色的是正六邊形，如
果我們近似把足球看成一個多面體．
（1）設黑色的正五邊形有x塊，則白色的正六邊形有（32﹣x）塊，當把足球看成一個多面體時，它的棱數是 ，它的頂點數是 ．
（2）求出黑皮和白皮各有多少塊？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠B＝90°，AB＝7 cm，AC＝25 cm.點P從點A沿AB方向以1 cm/s的速度運動至點B，點Q從點B沿BC方向以6 cm/s的速度運動至點C，P，Q兩點同時出發．
(1)求BC的長；
(2)當點P，Q運動2 s時，求P，Q兩點之間的距離；
(3)P，Q兩點運動幾秒時，AP＝CQ?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，點D、E、F分別在AB、BC、AC邊上，且BE=CF，BD=CE.
（1）求證：△DEF是等腰三角形；
（2）當∠A=40°時，求∠DEF的度數；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】A、B、C 為數軸上三點，若點 C 到點 A 的距離是點 C 到點 B 的距離的 2倍，則稱點 C 是（A，B）的奇異點，例如圖 1 中，點 A 表示的數為﹣1，點B 表示的數為 2，表示 1 的點 C 到點 A 的距離為 2，到點 B 的距離為 1，則點C 是（A，B）的奇異點，但不是（B，A）的奇異點．
(1)在圖 1 中，直接說出點 D 是（A，B）還是（B，C）的奇異點；
(2)如圖 2，若數軸上 M、N 兩點表示的數分別為﹣2 和 4，（M，N）的奇異點 K 在 M、N 兩點之間，請求出 K 點表示的數；
(3)如圖 3，A、B 在數軸上表示的數分別為﹣20 和 40，現有一點 P 從點 B 出發，向左運動．
①若點 P 到達點 A 停止，則當點 P 表示的數為多少時，P、A、B 中恰有一個點為其余兩點的奇異點？
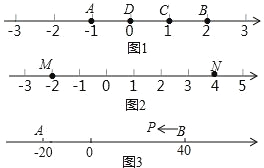
②若點 P 到達點 A 后繼續向左運動，是否存在使得 P、A、B 中恰有一個點為其余兩點的奇異點的情況？若存在，請直接寫出此時 PB 的距離；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com