
【題目】大石橋市政府為了落實“暖冬惠民工程”,計劃對城區內某小區的部分老舊房屋及供暖管道和部分路段的人行地磚、綠化帶等公共設施進行全面更新改造。該工程乙隊單獨完成所需天數是甲隊單獨完成所需天數的1.5倍 , 若甲隊先做10天,剩下兩隊合作30天完成。
(1)甲乙兩個隊單獨完成此項工程各需多少天?
(2)已知甲隊每天的施工費用為8.4萬元,乙對每天的施工費用為5.6萬元,工程施工的預算費用為500萬元,為了縮短工期并高效完成工程,擬預算的費用是否夠用?若不夠用,需追加預算多少萬元?請說明理由。
【答案】(1)甲隊單獨完成此項工程需要60天,乙隊單獨完成此項工程需要90天;(2)工程預算的施工費用不夠用,需追加預算4萬元.
【解析】
(1)設甲單獨完成這項工程所需天數,表示出乙單獨完成這項工程所需天數及各自的工作效率.根據工作量=工作效率×工作時間列方程求解;
(2)根據題意,甲乙合作工期最短,所以須求合作的時間,然后計算費用,作出判斷.
(1)設此工程甲隊單獨完成需x天,則乙隊單獨完成這項工程需1.5x天.由題意:
![]()
解得:x=60.
經檢驗,x=60是原方程的解,且適合題意.
1.5x=1.5×60=90.
答:甲隊單獨完成此項工程需要60天,乙隊單獨完成此項工程需要90天.
(2)因為需要縮短工期并高效完成工程,所以需兩隊合作完成,設兩隊合作這項工程需
y天,根據題意得:
![]()
解得:y=36.
所以需要施工費用36×(8.4+5.6)=504(萬元).
因為504>500,所以工程預算的施工費用不夠用,需追加預算4萬元.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
【題目】問題:如圖(1),點E、F分別在正方形ABCD的邊BC、CD上,∠EAF=45°,試判斷BE、EF、FD之間的數量關系.
【發現證明】小聰把△ABE繞點A逆時針旋轉90°至△ADG,從而發現EF=BE+FD,請你利用圖(1)證明上述結論.
【類比引申】如圖(2),四邊形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,點E、F分別在邊BC、CD上,則當∠EAF與∠BAD滿足 關系時,仍有EF=BE+FD;請證明你的結論.
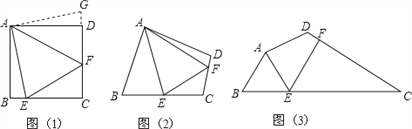
【探究應用】如圖(3),在某公園的同一水平面上,四條通道圍成四邊形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分別有景點E、F,且AE⊥AD,DF=40(![]() ﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長.(結果取整數,參考數據:
﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長.(結果取整數,參考數據: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若把邊長為1的正方形ABCD的四個角(陰影部分)剪掉,得一四邊形A1B1C1D1 . 試問怎樣剪,才能使剩下的圖形仍為正方形,且剩下圖形的面積為原來正方形面積的 ![]() ,請說明理由.(寫出證明及計算過程)
,請說明理由.(寫出證明及計算過程) 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A的坐標是(﹣1,0),點B的坐標是(9,0),以AB為直徑作⊙O′,交y軸的負半軸于點C,連接AC、BC,過A、B、C三點作拋物線.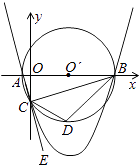
(1)求點C的坐標及拋物線的解析式;
(2)點E是AC延長線上一點,∠BCE的平分線CD交⊙O′于點D,求點D的坐標;并直接寫出直線BC、直線BD的解析式;
(3)在(2)的條件下,拋物線上是否存在點P,使得∠PDB=∠CBD,若存在,請求出點P的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家商店要進行裝修,若請甲、乙兩個裝修組同時施工,8天可以完成,需付兩組費用共3520元;若先請甲組單獨做6天,再請乙組單獨做12天可完成,需付兩組費用共3480元,問:
(1)甲、乙兩組工作一天,商店應各付多少元?
(2)已知甲組單獨做需12天完成,乙組單獨做需24天完成,單獨請哪組,商店所付費用最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵市民節約用水,某市水費實行階梯式計量水價.每戶每月用水量不超過25噸,收
費標準為每噸a元;若每戶每月用水量超過25噸時,其中前25噸還是每噸a元,超出的部
分收費標準為每噸b元.下表是小明家一至四月份用水量和繳納水費情況.根據表格提供的數
據,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(噸) | 16 | 18 | 30 | 35 |
水費(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32噸,則應繳水費 元;
(3)若小明家六月份應繳水費102.5元,則六月份他們家的用水量是多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知在數軸上有A、 B兩點,點A表示的數是-6,點B表示的數是9.點P在數軸上從點A出發,以每秒2個單位的速度沿數軸正方向運動,同時,點Q在數軸上從點B出發,以每秒3個單位的速度沿數軸負方向運動,當點Q到達點A時,兩點同時停止運動,設運動時間為t秒.
(1) AB=____ ;當t=1時,點Q表示的數是___ ;當t=___時,P、Q兩點相遇;
(2)如圖2,若點M為線段AP的中點,點N為線段BP中點,點P在運動過程中,線段MN的長度是否發生變化?若變化,請說明理由.若不變,請求出線段MN的長;
(3)如圖3,若點M為線段的AP中點,點T為線段BQ中點,則點M表示的數為______;點T表示的數為______;MT=______ (用含t的代數式填空).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班在一次班會課上,就“遇見路人摔倒后如何處理”的主題進行討論,并對全班 50 名學生的處理方式進行統計,得出相關統計表和統計圖.
組別 | A | B | C | D |
處理方式 | 迅速離開 | 馬上救助 | 視情況而定 | 只看熱鬧 |
人數 | m | 30 | n | 5 |
請根據表圖所提供的信息回答下列問題:
(1)統計表中的 m= ,n= ;
(2)補全頻數分布直方圖;
(3)若該校有 2000 名學生,請據此估計該校學生采取“馬上救助”方式的學生有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB∥CD,EF分別交AB、CD于G、F兩點,射線FM平分∠EFD,將射線FM平移,使得端點F與點G重合且得到射線GN.若∠EFC=110°,則∠AGN的度數是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com