
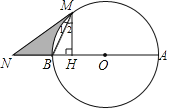
【題目】如圖,AB是⊙O的直徑,NM與⊙O相切于點M,與AB的延長線交于點N,MH⊥AB于點H.
(1)求證:∠1=∠2;
(2)若∠N=30°,BN=5,求⊙O的半徑;
(3)在(2)的條件下,求線段BN、MN及劣弧BM圍成的陰影部分面積.
【答案】(1)詳見解析;(2)⊙O的半徑為5;(3)![]()
【解析】
(1)根據切線的性質得出OM⊥MN,即可得出∠1+∠BMO=∠NMO=90°,由NH⊥AB,推出∠2+∠MBO=90°,根據等腰三角形的性質得出∠OBM=∠OMB,即可證得∠1=∠2;
(2)由∠N=30°,推出∠1+∠2=60°,所以∠1=∠2=30°,∠MON=60°,得到BM=BN=5,易知△OBM為等邊三角形,所以OB=OM=BM=5,得出結論;
(3)三角形OMN的面積減去扇形OMN的面積即為線段BN、MN及劣弧BM圍成的陰影部分面積.
解:(1)證明:連接OM,
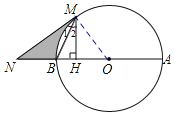
∵NM與⊙O相切,
∴OM⊥MN,
∵OB=OM,
∴∠OBM=∠OMB,
∵NH⊥AB,
∴∠2+∠MBO=90°,
∵∠1+∠BMO=∠NMO=90°,
∴∠1=∠2;
(2)∵∠N=30°,
MH⊥AB,
∴∠1+∠2=60°,
∴∠1=∠2=30°,∠MON=60°,
∴BM=BN=5,
∵OB=OM,
∴△OBM為等邊三角形,
∴OB=OM=BM=5,
即⊙O的半徑為5;
(3)由(2)知,∠N=30°,OM=5,
∴MN=5![]() ,
,
∴S△OMN=![]() MNOM=
MNOM=![]() =
=![]() ,
,
S扇形MOB=![]() =
=![]() ,
,
∴線段BN、MN及劣弧BM圍成的陰影部分面積=![]() .
.


科目:初中數學 來源: 題型:
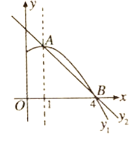
【題目】如圖是拋物線![]() 圖象的一部分,拋物線的頂點是
圖象的一部分,拋物線的頂點是![]() ,對稱軸是直線
,對稱軸是直線![]() ,且拋物線與
,且拋物線與![]() 軸的一個交點為
軸的一個交點為![]() ;直線
;直線![]() 的解析式為
的解析式為![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③方程
;③方程![]() 有兩個不相等的實數根;④拋物線與
有兩個不相等的實數根;④拋物線與![]() 軸的另一個交點是
軸的另一個交點是![]() ;⑤當
;⑤當![]() 時,則
時,則![]() .其中正確的是( )
.其中正確的是( )
A.①②B.①③⑤C.①④D.①④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
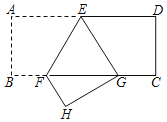
【題目】如圖,矩形ABCD中,點E,F分別在AD,BC上,且AE=DE,BC=3BF,連接EF,將矩形ABCD沿EF折疊,點A恰好落在BC邊上的點G處,則cos∠EGF的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】移動支付快捷高效,中國移動支付在世界處于領先水平,為了解人們平時最喜歡用哪種,移動支付支付方式,為此在某步行街,使用某app,軟件對使用移動支付的行人進行隨機抽樣調查,設置了四個選項,支付寶,微信,銀行卡,其他移動支付(每人只選一項),以下是根據調查結果分別整理的不完整的條形統計圖和扇形統計圖.
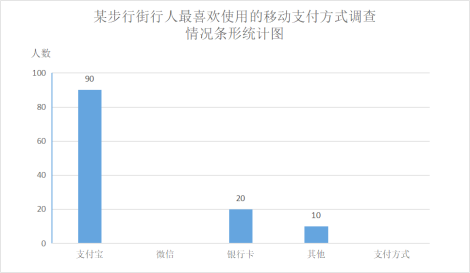

請你根據下列統計圖提供的信息,完成下列問題.
(1)這次調查的樣本容量是 ;
(2)請補全條形統計圖;
(3)求在此次調查中表示使用微信支付的扇形所對的圓心角的度數.
(4)若某天該步行街人流量為10萬人,其中40%的人購物并選擇移動支付,請你依據此次調查獲得的信息,估計一下當天使用銀行卡支付的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
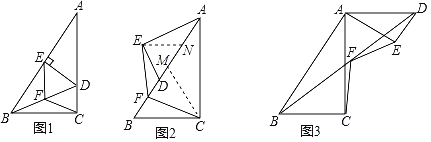
【題目】如圖1,△ABC是直角三角形,∠ACB=90°,點D在AC上,DE⊥AB于E,連接BD,點F是BD的中點,連接EF,CF.
(1)EF和CF的數量關系為 ;
(2)如圖2,若△ADE繞著點A旋轉,當點D落在AB上時,小明通過作△ABC和△ADE斜邊上的中線CM和EN,再利用全等三角形的判定,得到了EF和CF的數量關系,請寫出此時EF和CF的數量關系 ;
(3)若△AED繼續繞著點A旋轉到圖3的位置時,EF和CF的數量關系是什么?寫出你的猜想,并給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
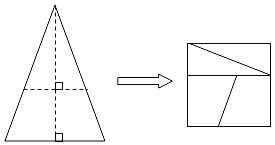
【題目】如圖,將等腰三角形紙片沿圖中虛線剪成四塊圖形,用這四塊圖形進行拼接,恰能拼成一個沒有縫隙的正方形,則正方形的邊長與等腰三角形的底邊長的比為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
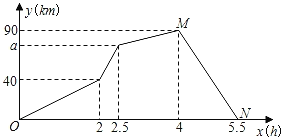
【題目】某快遞公司有甲、乙兩輛貨車沿同一路線從A地到B地配送貨物.某天兩車同時從A地出發,駛向B地,途中乙車由于出現故障,停車修理了一段時間,修理完畢后,乙車加快了速度勻速駛向B地;甲車從A地到B地速度始終保持不變.如圖所示是甲、乙兩車之間的距離y(km)與兩車出發時間x(h)的函數圖象.根據相關信息解答下列問題:
(1)點M的坐標表示的實際意義是什么?
(2)求出MN所表示的關系式,并寫出乙故障后的速度;
(3)求故障前兩車的速度以及a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AB=5cm,cosB![]() .動點D從點A出發沿著射線AC的方向以每秒1cm的速度移動,動點E從點B出發沿著射線BA的方向以每秒2cm的速度移動.已知點D和點E同時出發,設它們運動的時間為t秒.聯結BD.
.動點D從點A出發沿著射線AC的方向以每秒1cm的速度移動,動點E從點B出發沿著射線BA的方向以每秒2cm的速度移動.已知點D和點E同時出發,設它們運動的時間為t秒.聯結BD.
(1)當AD=AB時,求tan∠ABD的值;
(2)以A為圓心,AD為半徑畫⊙A;以點B為圓心、BE為半徑畫⊙B.討論⊙A與⊙B的位置關系,并寫出相對應的t的值.
(3)當△BDE為直角三角形時,直接寫出tan∠CBD的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從青島到濟南有南線和北線兩條高速公路:南線全長400千米,北線全長320千米.甲、乙兩輛客車分別由南線和北線從青島駛往濟南,已知客車甲在南線高速公路上行駛的平均速度比客車乙在北線高速公路上快20千米/小時,兩車恰好同時到達濟南,求兩輛客車從青島到濟南所用的時間是多少小時?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com