【題目】如圖，點A在∠O的一邊OA上．按要求畫圖并填空：
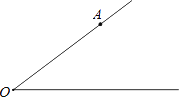
（1）過點A畫直線AB⊥OA，與∠O的另一邊相交于點B；過點A畫OB的垂線段AC，垂足為點C；過點C畫直線CD∥OA，交直線AB于點D。
（2）∠CDB=________°；
（3）如果OA=8，AB=6，OB=10，則點A到直線OB的距離為________．
科目：初中數學 來源： 題型：
【題目】去年春季，蔬菜種植場在15公頃的大棚地里分別種植了茄子和西紅柿，總費用是
萬元
其中，種植茄子和西紅柿每公頃的費用和每公頃獲利情況如表：
每公頃費用 | 每公頃獲利 | |
茄子 |
|
|
西紅柿 |
|
|
請解答下列問題：
求出茄子和西紅柿的種植面積各為多少公頃？
種植場在這一季共獲利多少萬元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形ABCD的對角線相交于點O，點M，N分別是邊BC，CD上的動點（不與點B，C，D重合），AM，AN分別交BD于點E，F，且∠MAN始終保持45°不變．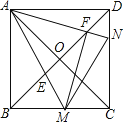
（1）求證： 
= 
；
（2）求證：AF⊥FM；
（3）請探索：在∠MAN的旋轉過程中，當∠BAM等于多少度時，∠FMN=∠BAM？寫出你的探索結論，并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如下數表是由從1開始的連續自然數組成，觀察規律并完成各題的解答．
（1）表中第8行的最后一個數是 ，它是自然數 的平方，第8行共有 個數；
（2）用含n的代數式表示：第n行的第一個數是 ，最后一個數是 ，第n行共有 個數；
（3）求第n行各數之和．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知P1（x1，y1），P2（x2，y2），P3（x3，y3）是反比例函數
的圖象上的三點，且x1＜0＜x2＜x3，則y1，y2，y3的大小關系是________.
【答案】
【解析】試題分析：∵函數y＝
中，k＝－1＜0，
∴此函數的圖象的兩個分支位于二四象限，且在每一象限內，y隨x的增大而增大．
∵x1＜0＜x2＜x3，
∴點A（x1，y1）在第二象限，B（x2，y2）、C（x3，y3）在第四象限，
∴y1＞0，y2＜y3＜0，
∴y2＜y3＜y1．
故答案為：y2＜y3＜y1．
點睛：本題考查的是反比例函數圖象的性質，當k＞0時，圖象位于一三象限，在每一個象限內y隨x的增大而減小，k＜0時，圖象位于二四象限，在每一個象限內，y隨x的增大而增大．
【題型】填空題
【結束】
14
【題目】如圖,直線y=kx(k<0)與雙曲線
交于A(x1，y1)，B(x2，y2)兩點,則3x1y2-5x2y1的值為 __________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】解分式方程：
(1) 
(2) 
【答案】(1) 
;(2)x=
【解析】試題分析：（1）兩邊乘以(x－1)(2x＋1)去分母，轉化為整式方程，然后解整式方程，檢驗后寫出分式方程的解即可；
（2）兩邊乘以(x＋2)(x－2)去分母，轉化為整式方程，然后解整式方程，檢驗后寫出分式方程的解即可．
試題解析：
解：（1）兩邊乘以(x－1)(2x＋1)去分母得：2x＋1＝5(x－1)，
解得：x＝2，
當x＝2時，(x－1)(2x＋1)≠0，
∴原分式方程的解為x＝2；
（2）兩邊乘以(x＋2)(x－2)去分母得：(x－2)2－3＝(x＋2)(x－2)，
解得：x＝
，
當x＝
時，(x＋2)(x－2)≠0，
所以原分式方程的解為x＝
．
【題型】解答題
【結束】
21
【題目】先化簡，再求值
，其中
的值從不等式組
的整數解中選取.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=﹣ 
x2﹣ 
x+2與x軸交于A、B兩點，與y軸交于點C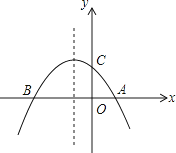 
（1）求點A，B，C的坐標；
（2）點E是此拋物線上的點，點F是其對稱軸上的點，求以A，B，E，F為頂點的平行四邊形的面積；
（3）此拋物線的對稱軸上是否存在點M，使得△ACM是等腰三角形？若存在，請求出點M的坐標；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
