
【題目】綜合題
(1)![]()
.
(2)解分式方程: ![]()
【答案】
(1)
解: ![]()
原式= ![]()
= ![]()
(2)
解:解分式方程: ![]()
去分母,得x-2(x-3)=4
去括號,得x-2x+6=4
移項,得x-2x=4-6
合并同類項,得-x=-2
解方程得x=2
經檢驗:x=2是原分式方程的根
解方程得x=2
經檢驗:x=2是原分式方程的根
【解析】(1)所有非零數的0次冪都等于1,sin45°=![]() ;去絕對值符號時,要注意負數的絕對值是它的相反數;
;去絕對值符號時,要注意負數的絕對值是它的相反數;
(2)解分式方程:去分母,去括號,移項,合并同類項,未知數系數化為1,檢驗方程的解.
【考點精析】通過靈活運用去分母法和特殊角的三角函數值,掌握先約后乘公分母,整式方程轉化出.特殊情況可換元,去掉分母是出路.求得解后要驗根,原留增舍別含糊;分母口訣:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口訣:“123,321,三九二十七”即可以解答此題.


科目:初中數學 來源: 題型:
【題目】如圖所示,已知△ABC的三個頂點的坐標分別為A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)請直接寫出點B關于點A對稱的點的坐標;
(2)將△ABC繞坐標原點O逆時針旋轉90°,畫出圖形,直接寫出點B的對應點的坐標;
(3)請直接寫出:以A、B、C為頂點的平行四邊形的第四個頂點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
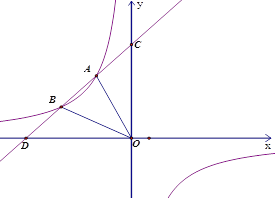
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象相交于A,B兩點,且與坐標軸的交點為(﹣6,0),(0,6),點B的橫坐標為﹣4.點A的縱坐標為4.
的圖象相交于A,B兩點,且與坐標軸的交點為(﹣6,0),(0,6),點B的橫坐標為﹣4.點A的縱坐標為4.
(1)試確定反比例函數的解析式;
(2)求△AOB的面積;
(3)直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將斜邊長為4的直角三角板放在直角坐標系xOy中,兩條直角邊分別與坐標軸重合,P為斜邊的中點.現將此三角板繞點O順時針旋轉120°后點P的對應點的坐標是( )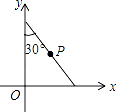
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列各式:13=1=![]() ;13+23=9=
;13+23=9=![]() ;13+23+33=36=
;13+23+33=36=![]() ;13+23+33+43=100=
;13+23+33+43=100=![]() ,
,
回答下面的問題:
(1)13+23+33+43+…+103=_____(寫出算式即可);
(2)計算13+23+33+…+993+1003的值;
(3)計算:113+123+…+993+1003的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=﹣x2+bx+c經過A(﹣1,0),B(4,0)兩點,與y軸相交于點C,連結BC,點P為拋物線上一動點,過點P作x軸的垂線l,交直線BC于點G,交x軸于點E.
(1)求拋物線的表達式;
(2)當P位于y軸右邊的拋物線上運動時,過點C作CF⊥直線l,F為垂足,當點P運動到何處時,以P,C,F為頂點的三角形與△OBC相似?并求出此時點P的坐標;
(3)如圖2,當點P在位于直線BC上方的拋物線上運動時,連結PC,PB,請問△PBC的面積S能否取得最大值?若能,請求出最大面積S,并求出此時點P的坐標,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,CD、C′D′分別是Rt△ABC,Rt△A′B′C′斜邊上的高,且CB=C′B′,CD=C′D′.求證:△ABC≌△A′B′C′.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形 ABCD 的對角線 AC 與 BD 相交于點 O,CE∥BD,DE∥AC.
(1)求證:四邊形 OCED 為菱形
(2)若AD=7,AB=4,求四邊形 OCED的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com