
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
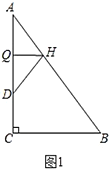
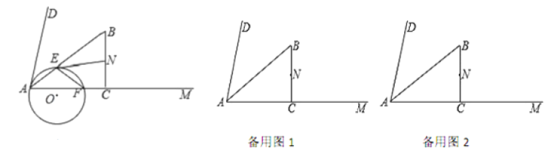
(1)如圖1,折疊![]() 使點(diǎn)
使點(diǎn)![]() 落在
落在![]() 邊上的點(diǎn)
邊上的點(diǎn)![]() 處,折痕交
處,折痕交![]() 、
、![]() 分別于點(diǎn)
分別于點(diǎn)![]() 、
、![]() ,若
,若![]() ,則
,則![]() ________.
________.
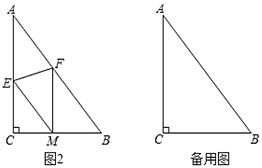
(2)如圖2,折疊![]() 使點(diǎn)
使點(diǎn)![]() 落在
落在![]() 邊上的點(diǎn)
邊上的點(diǎn)![]() 處,折痕交
處,折痕交![]() 、
、![]() 分別于點(diǎn)
分別于點(diǎn)![]() 、
、![]() .若
.若![]() ,求證:四邊形
,求證:四邊形![]() 是菱形;
是菱形;
(3)在(1)(2)的條件下,線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 的長(zhǎng);若不存在,請(qǐng)說(shuō)明理由.
的長(zhǎng);若不存在,請(qǐng)說(shuō)明理由.
【答案】(1)5;(2)見(jiàn)解析;(3)存在,滿足條件長(zhǎng)![]() 的值為
的值為![]() 或10或
或10或![]() .
.
【解析】
(1)利用勾股定理求出AC,設(shè)HQ=x,根據(jù)![]() ,構(gòu)建方程即可解決問(wèn)題;
,構(gòu)建方程即可解決問(wèn)題;
(2)由翻折的性質(zhì)可得![]() ,
,![]() ,然后證明出
,然后證明出![]() 即可;
即可;
(3)設(shè)AE=EM=FM=AF=4m,則BM=3m,FB=5m,構(gòu)建方程求出m的值,然后根據(jù)![]() ,
,![]() ,求出
,求出![]() ,設(shè)
,設(shè)![]() ,分兩種情形分別求解即可解決問(wèn)題.
,分兩種情形分別求解即可解決問(wèn)題.
解:(1)在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
設(shè)![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或-5(舍棄),
或-5(舍棄),
∴![]() ,
,
故答案為5;
(2)由翻折的性質(zhì)可知:![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四邊形![]() 是菱形;
是菱形;
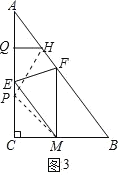
(3)如圖3中,設(shè)![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
設(shè)![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∴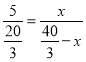 ,解得:
,解得:![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∴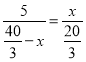 ,解得:
,解得:![]() 或
或![]() ,
,
經(jīng)檢驗(yàn):![]() 或
或![]() 是分式方程的解,且符合題意,
是分式方程的解,且符合題意,
綜上所述,滿足條件的![]() 的長(zhǎng)為
的長(zhǎng)為![]() 或10或
或10或![]() .
.


 名牌學(xué)校分層周周測(cè)系列答案
名牌學(xué)校分層周周測(cè)系列答案 黃岡海淀全程培優(yōu)測(cè)試卷系列答案
黃岡海淀全程培優(yōu)測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
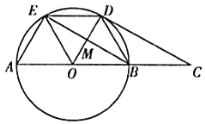
【題目】如圖所示,![]() 的直徑
的直徑![]() ,
,![]() 、
、![]() 為圓周上兩點(diǎn),且
為圓周上兩點(diǎn),且![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() ,交
,交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() .
.
(1)求證:![]() 為
為![]() 切線;
切線;
(2)填空:①當(dāng)四邊形![]() 為菱形,則
為菱形,則![]() 的度數(shù)為________;
的度數(shù)為________;
②當(dāng)![]() 時(shí),四邊形
時(shí),四邊形![]() 的面積為________.
的面積為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】綜合與實(shí)踐 在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 為斜邊
為斜邊![]() 上的動(dòng)點(diǎn)(不與點(diǎn)
上的動(dòng)點(diǎn)(不與點(diǎn)![]() 重合).
重合).
(1)操作發(fā)現(xiàn): 如圖①,當(dāng)![]() 時(shí),把線段
時(shí),把線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 得到線段
得到線段![]() ,連接
,連接![]() .
.
①![]() 的度數(shù)為________;
的度數(shù)為________;
②當(dāng)![]() ________時(shí),四邊形
________時(shí),四邊形![]() 為正方形;
為正方形;

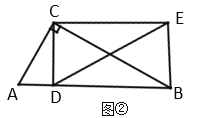
(2)探究證明: 如圖②,當(dāng)![]() 時(shí),把線段
時(shí),把線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 后并延長(zhǎng)為原來(lái)的兩倍, 記為線段
后并延長(zhǎng)為原來(lái)的兩倍, 記為線段![]() ,連接
,連接![]() .
.
①在點(diǎn)![]() 的運(yùn)動(dòng)過(guò)程中,請(qǐng)判斷
的運(yùn)動(dòng)過(guò)程中,請(qǐng)判斷![]() 與
與![]() 的大小關(guān)系,并證明;
的大小關(guān)系,并證明;
②當(dāng) 時(shí),求證:四邊形
時(shí),求證:四邊形![]() 為矩形.
為矩形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
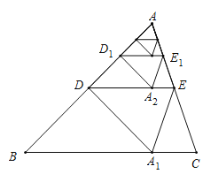
【題目】如圖,將![]() 沿著過(guò)
沿著過(guò)![]() 中點(diǎn)
中點(diǎn)![]() 的直線折疊,使點(diǎn)
的直線折疊,使點(diǎn)![]() 落在
落在![]() 邊上的
邊上的![]() ,稱為第
,稱為第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距離記為
的距離記為![]() ;還原紙片后,再將
;還原紙片后,再將![]() 沿著過(guò)
沿著過(guò)![]() 中點(diǎn)
中點(diǎn)![]() 的直線折疊,使點(diǎn)
的直線折疊,使點(diǎn)![]() 落在
落在![]() 邊上的
邊上的![]() 處,稱為第
處,稱為第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距離記為
的距離記為![]() ;按上述方法不斷操作下去…,經(jīng)過(guò)第
;按上述方法不斷操作下去…,經(jīng)過(guò)第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距離記為
的距離記為![]() ,若
,若![]() ,則
,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商品原價(jià)為100元,第一次漲價(jià)![]() ,第二次在第一次的基礎(chǔ)上又漲價(jià)
,第二次在第一次的基礎(chǔ)上又漲價(jià)![]() ,設(shè)平均每次增長(zhǎng)的百分?jǐn)?shù)為x,那么x應(yīng)滿足的方程是
,設(shè)平均每次增長(zhǎng)的百分?jǐn)?shù)為x,那么x應(yīng)滿足的方程是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了解某中學(xué)學(xué)生課余生活情況,對(duì)喜愛(ài)看課外書(shū)、體育活動(dòng)、看電視、社會(huì)實(shí)踐四個(gè)方面的人數(shù)進(jìn)行調(diào)查統(tǒng)計(jì),現(xiàn)從該校隨機(jī)抽取n名學(xué)生作為樣本,采用問(wèn)卷調(diào)查的方式收集數(shù)據(jù)![]() 參與問(wèn)卷調(diào)查的每名學(xué)生只能選擇其中一項(xiàng)
參與問(wèn)卷調(diào)查的每名學(xué)生只能選擇其中一項(xiàng)![]() ,并根據(jù)調(diào)查得到的數(shù)據(jù)繪制成了如圖所示的兩幅不完整的統(tǒng)計(jì)圖,由圖中提供的信息,解答下列問(wèn)題:
,并根據(jù)調(diào)查得到的數(shù)據(jù)繪制成了如圖所示的兩幅不完整的統(tǒng)計(jì)圖,由圖中提供的信息,解答下列問(wèn)題:

![]() 補(bǔ)全條形統(tǒng)計(jì)圖;
補(bǔ)全條形統(tǒng)計(jì)圖;
![]() 若該校共有學(xué)生2400名,試估計(jì)該校喜愛(ài)看電視的學(xué)生人數(shù).
若該校共有學(xué)生2400名,試估計(jì)該校喜愛(ài)看電視的學(xué)生人數(shù).
![]() 若調(diào)查到喜愛(ài)體育活動(dòng)的4名學(xué)生中有3名男生和1名女生,現(xiàn)從這4名學(xué)生中任意抽取2名,求恰好抽到2名男生的概率.
若調(diào)查到喜愛(ài)體育活動(dòng)的4名學(xué)生中有3名男生和1名女生,現(xiàn)從這4名學(xué)生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD是矩形,把矩形沿AC折疊,點(diǎn)B落在點(diǎn)E處,AE與DC的交點(diǎn)為O,連接DE.
(1)求證:△ADE≌△CED;
(2)求證:DE∥AC.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市對(duì)即將參加中考的4000名初中畢業(yè)生進(jìn)行了一次視力抽樣調(diào)查,繪制出頻數(shù)分布表和不完整的頻數(shù)分布直方圖.請(qǐng)根據(jù)圖表信息回答下列問(wèn)題:
初中畢業(yè)生視力抽樣調(diào)查頻數(shù)分布表
視力 | 頻數(shù)(人) | 頻率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次調(diào)查樣本容量為 ;
(2)在頻數(shù)分布表中,a= ,b= ,并將頻數(shù)分布直方圖補(bǔ)充完整;
(3)若視力在4.9以上(含4.9)均屬標(biāo)準(zhǔn)視力,根據(jù)上述信息估計(jì)全區(qū)初中畢業(yè)生中達(dá)到標(biāo)準(zhǔn)視力的學(xué)生約有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 內(nèi)部做
內(nèi)部做![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn):動(dòng)點(diǎn)
的中點(diǎn):動(dòng)點(diǎn)![]() 由
由![]() 出發(fā),沿
出發(fā),沿![]() 運(yùn)動(dòng),速度為每秒5個(gè)單位,動(dòng)點(diǎn)
運(yùn)動(dòng),速度為每秒5個(gè)單位,動(dòng)點(diǎn)![]() 由
由![]() 出發(fā),沿
出發(fā),沿![]() 運(yùn)動(dòng),速度為每秒8個(gè)單位,當(dāng)點(diǎn)
運(yùn)動(dòng),速度為每秒8個(gè)單位,當(dāng)點(diǎn)![]() 到達(dá)點(diǎn)
到達(dá)點(diǎn)![]() 時(shí),兩點(diǎn)同時(shí)停止運(yùn)動(dòng);過(guò)
時(shí),兩點(diǎn)同時(shí)停止運(yùn)動(dòng);過(guò)![]() 、
、![]() 、
、![]() 作
作![]() ;
;
(1)判斷![]() 的形狀為________,并判斷
的形狀為________,并判斷![]() 與
與![]() 的位置關(guān)系為__________;
的位置關(guān)系為__________;
(2)求![]() 為何值時(shí),
為何值時(shí),![]() 與
與![]() 相切?求出此時(shí)
相切?求出此時(shí)![]() 的半徑,并比較半徑與劣弧
的半徑,并比較半徑與劣弧![]() 長(zhǎng)度的大小;
長(zhǎng)度的大小;
(3)直接寫(xiě)出![]() 的內(nèi)心運(yùn)動(dòng)的路徑長(zhǎng)為__________;(注:當(dāng)
的內(nèi)心運(yùn)動(dòng)的路徑長(zhǎng)為__________;(注:當(dāng)![]() 、
、![]() 、
、![]() 重合時(shí),內(nèi)心就是
重合時(shí),內(nèi)心就是![]() 點(diǎn))
點(diǎn))
(4)直接寫(xiě)出線段![]() 與
與![]() 有兩個(gè)公共點(diǎn)時(shí),
有兩個(gè)公共點(diǎn)時(shí),![]() 的取值范圍為__________.
的取值范圍為__________.
(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com