
【題目】下列說法:①若![]() =﹣1,則a、b互為相反數;②若a+b<0,且
=﹣1,則a、b互為相反數;②若a+b<0,且![]() >0,則|a+2b|=﹣a﹣2b;③一個數的立方是它本身,則這個數為0或1;④若﹣1<a<0,則a2>﹣
>0,則|a+2b|=﹣a﹣2b;③一個數的立方是它本身,則這個數為0或1;④若﹣1<a<0,則a2>﹣![]() ;⑤若a+b+c<0,ab>0,c>0,則|﹣a|=﹣a,其中正確的個數是( )
;⑤若a+b+c<0,ab>0,c>0,則|﹣a|=﹣a,其中正確的個數是( )
A. 2個 B. 3個 C. 4個 D. 5個
【答案】B
【解析】
先去分母,變形后根據相反數的定義即可判斷①;先確定A、B是負數,再求出a+2b<0,根據絕對值的性質判斷②即可;根據立方根的性質判斷③即可;取a=-![]() ,分別求出a2和-
,分別求出a2和-![]() 的值,再判斷④即可;先求出a<0,再判斷⑤即可.
的值,再判斷④即可;先求出a<0,再判斷⑤即可.
解:∵![]() =-1,
=-1,
∴a=-b,
∴a+b=0,
即a、b互為相反數,故①正確;
∵a+b<0,且![]() >0,
>0,
∴a、b都是負數,
∴a+2b<0,
∴|a+2b|=-a-2b,故②正確;
一個數的立方是它本身,則這個數為0或1或-1,故③錯誤;
∵-1<a<0,
∴取a=-![]() ,
,
則a2=![]() ,-
,-![]() =2,
=2,
∴a2<-![]() ,故④錯誤;
,故④錯誤;
∵ab>0,
∴a、b同號,
∵a+b+c<0,c>0,
∴a、b都是負數,
∴|-a|=-a,故⑤正確;
即正確的個數是3個,
故選:B.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,以AC為直徑作⊙O交BC于點D,交AB于點G,且D是BC的中點,DE⊥AB,垂足為E,交AC的延長線于點F. 
(1)求證:直線EF是⊙O的切線;
(2)CF=5,cos∠A= ![]() ,求AE的長.
,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC中,AC=BC,∠ACB=90°,過點C作CD⊥AB于點D,點E是AB邊上一動點(不含端點A,B),連接CE,過點B作CE的垂線交直線CE于點F,交直線CD于點G.
(1)求證:AE=CG;
(2)若點E運動到線段BD上時(如圖②),試猜想AE,CG的數量關系是否發生變化,請寫出你的結論;
(3)過點A作AH⊥CE,垂足為點H,并交CD的延長線于點M(如圖③),找出圖中與BE相等的線段,并證明.
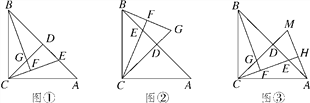
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,己知△ABC,任取一點O,連AO,BO,CO,并取它們的中點D,E,F,得△DEF,則下列說法正確的個數是( ) ①△ABC與△DEF是位似圖形; ②△ABC與△DEF是相似圖形;
③△ABC與△DEF的周長比為1:2;④△ABC與△DEF的面積比為4:1.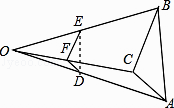
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五一期間,小明一家一起去旅游,如圖是小明設計的某旅游景點的圖紙(網格是由相同的小正方形組成的,且小正方形的邊長代表實際長度100m),在該圖紙上可看到兩個標志性景點A,B.若建立適當的平面直角坐標系,則點A(-3,1),B(-3,-3),第三個景點C(3,2)的位置已破損.
(1)請在圖中標出景點C的位置;
(2)小明想從景點B開始游玩,途經景點A,最后到達景點C,求小明一家最短的行走路程(參考數據:![]() ≈6,結果保留整數).
≈6,結果保留整數).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:數軸上有A、B兩點,分別對應的數為a,b,已知(a+1)2與|b﹣3|互為相反數.點P為數軸上一動點,對應為x.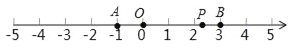
(1)a= ;b=
(2)若點P到點A和點B的距離相等,則點P對應的數是
(3)數軸上是否存在點P,使點P到點A和點B的距離之和為5?若存在,請求出x的值;若不存在,說明理由;
(4)|x﹣a|+|x﹣b|的最小值=
(5)當點P以每分鐘1個單位長度的速度從O點向左運動,點A以每分鐘5個單位長度向左運動,問幾分鐘時點P到點A、點B的距離相等?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=8,AD=5,點E![]() 為DC邊上一個動點,把△ADE沿AE折疊,點D的對應點D’落在矩形ABCD的對稱軸上時,DE的長為____________.
為DC邊上一個動點,把△ADE沿AE折疊,點D的對應點D’落在矩形ABCD的對稱軸上時,DE的長為____________.
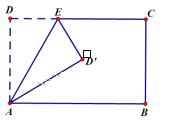
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E在AB邊上,沿CE折疊矩形ABCD,使點B落在AD邊上的點F處,若AB=4,BC=5,則tan∠AFE的值為( ) 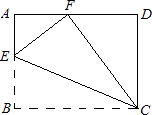
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com