
【題目】已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).
(1)畫出△ABC向下平移4個單位長度得到的△A1B1C1,點C1的坐標是 ;
(2)以點B為位似中心,在網格內畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為2:1,點C2的坐標是 ;
(3)△A2B2C2的面積是 平方單位.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,點E為BC邊的中點,點B′與點B關于AE對稱,B′B與AE交于點F,連接AB′,DB′,FC.下列結論:①AB′=AD;②△FCB′為等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.其中正確的是( )

A. ①② B. ①②④ C. ③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展“我的中國夢”演講比賽活動,九(1)、九(2)班根據初賽成績各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績(滿分為100分)如下圖所示.

(1)根據如圖,分別求出兩班復賽的平均成績和方差;
(2)根據(1)的計算結果,分析哪個班級5名選手的復賽成績波動小?
查看答案和解析>>
科目:初中數學 來源: 題型:
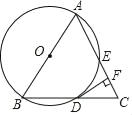
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O與BC交于點D,過點D作⊙O的切線與AC交于點F.
(1)求證:EF=CF;
(2)若AE=8,cosA=![]() ,求DF的長.
,求DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
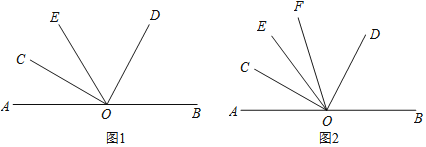
【題目】點O為直線AB上一點,在直線AB上側任作一個∠COD,使∠COD=90°.
(1)如圖1,過點O作射線OE,使OE是∠AOD的角平分線,求證:∠BOD=2∠COE;
(2)如圖2,過點O作射線OE,使OC是∠AOE的角平分線,另作射線OF,使OF是∠COD的平分線,若∠EOC=3∠EOF,求∠AOE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知y﹣2與x成正比例,當x=2時,y=6.
(1)求y與x之間的函數解析式.
(2)在所給直角坐標系中畫出函數圖象.
(3)由函數圖象直接寫出當﹣2≤y≤2時,自變量x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,直線y=x+b與雙曲線y=![]() (x<0)交于點A(﹣1,﹣5),并分別與x軸、y軸交于點C、B.
(x<0)交于點A(﹣1,﹣5),并分別與x軸、y軸交于點C、B.
(1)求出b、m的值;
(2)點D在x軸的正半軸上,若以點D、C、B組成的三角形與△OAB相似,試求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
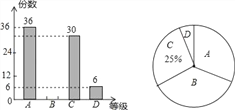
【題目】四川省第十三屆運動會將于2018年8月在我市舉行,某校組織了主題“我是運動會志愿者”的電子小報作品征集活動,先從中隨機抽取了部分作品,按A,B,C,D四個等級評分,然后根據統(tǒng)計結果繪制了如下兩幅不完整的統(tǒng)計圖,請根據圖中的信息,解答下列問題:
(1)求此次抽取的作品中等級為B的作品數,并補全條形統(tǒng)計圖;
(2)求扇形統(tǒng)計圖為D的扇形圓心角的度數;
(3)該校計劃從抽取的這些作品中選取部分作品參加市區(qū)的作品展.已知其中所選的到市區(qū)參展的A作品比B作品少4份,且A、B兩類作品數量和正好是本次抽取的四個等級作品數量的![]() ,求選取到市區(qū)參展的B類作品有多少份.
,求選取到市區(qū)參展的B類作品有多少份.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點A表示1,現將點A沿數軸做如下移動:第一次將點A向左移動3個單位長度到達點A1,第2次將點A1向右平移6個單位長度到達點A2,第3次將點A2向左移動9個單位長度到達點A3…則第6次移動到點A6時,點A6在數軸上對應的實數是_____;按照這種規(guī)律移動下去,至少移動_____次后該點到原點的距離不小于41.
![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com