Question

如圖，直線a、b、c表示三條公路，現要建一個貨物中轉站，要求它到三條公路的距離相等，則可供選擇的地址有      處.

Answer 1

4

此題考查了角平分線的性質
由三角形內角平分線的交點到三角形三邊的距離相等，可得三角形內角平分線的交點滿足條件；然后利用角平分線的性質，可證得三角形兩條外角平分線的交點到其三邊的距離也相等，這樣的點有3個，可得可供選擇的地址有4個．
∵△ABC內角平分線的交點到三角形三邊的距離相等，
∴△ABC內角平分線的交點滿足條件；
如圖：點P是△ABC兩條外角平分線的交點，過點P作PE⊥AB，PD⊥BC，PF⊥AC，

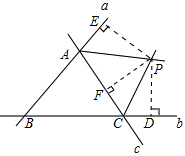
∴PE=PF，PF=PD，
∴PE=PF=PD，
∴點P到△ABC的三邊的距離相等，
∴△ABC兩條外角平分線的交點到其三邊的距離也相等，滿足這條件的點有3個；
綜上，到三條公路的距離相等的點有4個，
∴可供選擇的地址有4個．