
已知:如圖, AB是⊙O的直徑,AM和BN是⊙O的兩條切線,點D是AM上一點,聯結OD , 作BE∥OD交⊙O于點E, 聯結DE并延長交BN于點C.
(1)求證:DC是⊙O的切線;
(2)若AD=l,BC=4,求直徑AB的長.

(1)證明見解析;(2)4.
【解析】
試題分析:(1)連接OE,由OE=OB,利用等邊對等角得到一對角相等,再由OD與BE平行,得到一對同位角及一對內錯角相等,等量代換得到∠AOD=∠OBE=∠OEB=∠EOD,再由OA=OE,OD=OD,利用SAS得到三角形AOD與三角形EOD全等,由全等三角形對應角相等得到∠OAD=∠OED,根據AM為圓O的切線,利用切線的性質得到∠OAD=∠OED=90°,即可得證.
(2)過點D作BC的垂線,垂足為H,由BN與圓O切線于點B,得到∠ABC=90°=∠BAD=∠BHD,利用三個角為直角的四邊形為矩形得到ADHB為矩形,利用矩形的對邊相等得到BH=AD=1,AB=DH,由BC-BH求出HC的長,AD、CB、CD分別切⊙O于點A、B、E,利用切線長定理得到AD=DE=1,EC=BC=4,在直角三角形DHC中,利用勾股定理求出DH的長,即為AB的長.
試題解析:(1)如圖,連接OE,
在⊙O中,OA=OE=OB,∴∠OBE=∠OEB.
∵OD∥BE,∴∠AOD=∠OBE=∠OEB=∠EOD.
在△AOD和△EOD中,OA=OE,∠AOD=∠EOD,OD=OD,
∴△AOD≌△EOD(SAS).∴∠OAD=∠OED.
∵AM是⊙O的切線,切點為A,∴BA⊥AM.
∴∠OAD=∠OED=90°.∴OE⊥DE.
∵OE是⊙O的半徑,∴DE是⊙O的切線.
(2)如圖,過點D作BC的垂線,垂足為H,
∵BN切⊙O于點B,∴∠ABC=90°=∠BAD=∠BHD.∴四邊形ABHD是矩形.
∴AD=BH=1,AB=DH,∴CH=BC-BH=4-1=3.
∵AD、CB、CD分別切⊙O于點A、B、E,∴AD=ED=1,BC=CE=4.
∴DC=DE+CE=1+4=5,
在Rt△DHC中,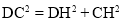 ,
,
∴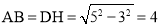 .
.

考點:1.切線的判定和性質;2.全等三角形的判定和性質;3.勾股定理,4.等腰三角形的性質;5.平行的性質;6.矩形的判定和性質.


科目:初中數學 來源:2013-2014學年北京市昌平區中考一模數學試卷(解析版) 題型:解答題
無論k取任何實數,對于直線 都會經過一個固定的點
都會經過一個固定的點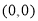 ,我們就稱直線
,我們就稱直線 恒過定點
恒過定點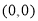 .
.
(1)無論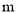 取任何實數,拋物線
取任何實數,拋物線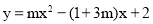 恒過定點
恒過定點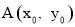 ,直接寫出定點A的坐標;
,直接寫出定點A的坐標;
(2)已知△ABC的一個頂點是(1)中的定點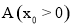 ,且∠B,∠C的角平分線分別是y軸和直線
,且∠B,∠C的角平分線分別是y軸和直線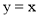 ,求邊BC所在直線的表達式;
,求邊BC所在直線的表達式;
(3)求△ABC內切圓的半徑.
查看答案和解析>>
科目:初中數學 來源:2013-2014學年北京市昌平區中考一模數學試卷(解析版) 題型:選擇題
如圖,在△ABC中,AB=AC,tan∠B=2, BC=3 . 邊AB上一動點M從點B出發沿B→A運動,動點N從點B出發沿B→C→A運動,在運動過程中,射線MN與射線BC交于點E,且夾角始終保持45°. 設BE=x, MN=y,則能表示y與x的函數關系的大致圖象是( )
. 邊AB上一動點M從點B出發沿B→A運動,動點N從點B出發沿B→C→A運動,在運動過程中,射線MN與射線BC交于點E,且夾角始終保持45°. 設BE=x, MN=y,則能表示y與x的函數關系的大致圖象是( )

A.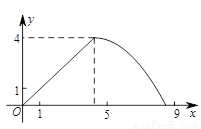
B. 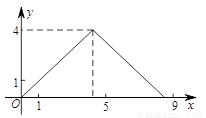
C. 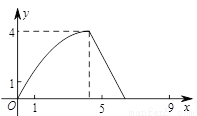
D. 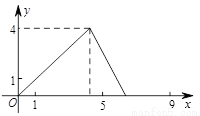
查看答案和解析>>
科目:初中數學 來源:2013-2014學年北京市昌平區中考一模數學試卷(解析版) 題型:選擇題
據統計,第22屆冬季奧林匹克運動會的電視轉播時間長達88000小時,社交網站和國際奧委會官方網站也創下冬奧會收看率紀錄. 用科學計數法表示88000為( )
A.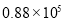 B.
B.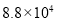 C.
C.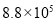 D.
D.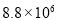
查看答案和解析>>
科目:初中數學 來源:2013-2014學年北京市豐臺區中考二模數學卷(解析版) 題型:解答題
某產品生產車間有工人10名.已知每名工人每天可生產甲種產品12個或乙種產品10個,且每生產一個甲種產品可獲利潤100元,每生產一個乙種產品可獲利潤180元.在這10名工人中,如果要使此車間每天所獲利潤不低于15600元,你認為至少要派多少名工人去生產乙種產品才合適.
查看答案和解析>>
科目:初中數學 來源:2013-2014學年內蒙古九年級6月中考模擬數學試卷(解析版) 題型:解答題
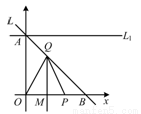
如圖,已知直線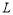 過點
過點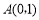 和
和 ,
,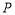 是
是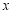 軸正半軸上的動點,
軸正半軸上的動點,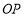 的垂直平分線交
的垂直平分線交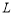 于點
于點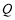 ,交
,交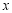 軸于點
軸于點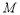 .
.
(1)直接寫出直線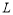 的解析式;
的解析式;
(2)當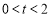 時,設
時,設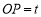 ,
,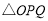 的面積為
的面積為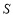 ,求S關于t的函數關系式;并求出S的最大值;
,求S關于t的函數關系式;并求出S的最大值;
(3)當點Q在線段AB上(Q與A、B不重合)時,直線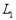 過點A且與x軸平行,問在
過點A且與x軸平行,問在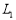 上是否存在點C,使得
上是否存在點C,使得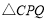 是以
是以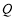 為直角頂點的等腰直角三角形?若存在,求出點C的坐標,并證明;若不存在,請說明理由.
為直角頂點的等腰直角三角形?若存在,求出點C的坐標,并證明;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com