
【題目】在平面直角坐標系![]() 中,圖形
中,圖形![]() 的投影矩形定義如下:矩形的兩組對邊分別平行于
的投影矩形定義如下:矩形的兩組對邊分別平行于![]() 軸,
軸,![]() 軸,圖形
軸,圖形![]() 的頂點在矩形的邊上或內部,且矩形的面積最小.設矩形的較長的邊與較短的邊的比為
的頂點在矩形的邊上或內部,且矩形的面積最小.設矩形的較長的邊與較短的邊的比為![]() ,我們稱常數
,我們稱常數![]() 為圖形
為圖形![]() 的投影比,如圖1,矩形
的投影比,如圖1,矩形![]() 為
為![]() 的投影矩形,其投影比
的投影矩形,其投影比![]() .
.
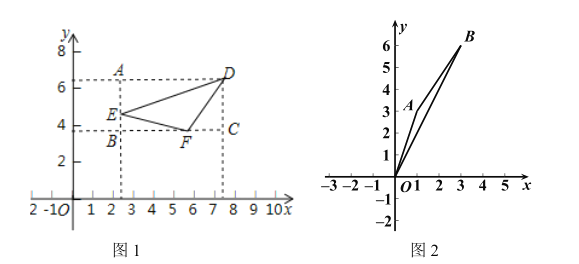
(1)如圖2,若點![]() ,則
,則![]() 投影比
投影比![]() 的值為________________;
的值為________________;
(2)已知點![]() ,點
,點![]() ,且
,且![]() 投影比
投影比![]() ,則
,則![]() 點坐標可能是__________(填寫序號);
點坐標可能是__________(填寫序號);
①![]() ②
②![]() ③
③![]() ④
④![]()
(3)已知點![]() ,在直線
,在直線![]() 上有一點
上有一點![]() 和一動點
和一動點![]() ,且
,且![]() ,是否存在這樣的
,是否存在這樣的![]() ,使得
,使得![]() 的投影比
的投影比![]() 為定值?若存在,請求出
為定值?若存在,請求出![]() 的范圍及定值
的范圍及定值![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
【答案】(1)2;(2)①②;(3)當m≤1時,k=2;當3≤m<5時,k=4.
【解析】
(1)在圖2中做出投影矩形,根據投影比可得到結論.
(2)根據每一個點作投影圖形,分別討論即可得到答案;
(3)根據題意畫出圖形,根據m的取值分類討論.
(1)如圖2,過點B作![]() 軸于點C,作
軸于點C,作![]() 軸于點D,則矩形OCBD為△OAB的投影矩形,
軸于點D,則矩形OCBD為△OAB的投影矩形,

∵![]() ,
,
∴OC=3,BC=6,
∴△OAB投影比k的值=2,.
(2)如圖,
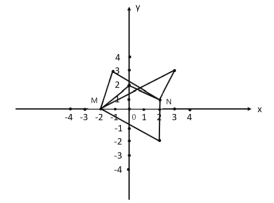
①點P的坐標為![]() 時,
時,![]() 投影比
投影比![]() ;
;
②點P的坐標為![]() 時,
時,![]() 投影比
投影比![]() ;
;
③點P的坐標為![]() 時,
時,![]() 投影比
投影比![]() ;
;
④點P的坐標為![]() 時,
時,![]() 投影比
投影比![]() ;
;
故答案是①②.
(3)在![]() 中,y=2時,則x=1;x=5時,y=10,
中,y=2時,則x=1;x=5時,y=10,
∴F(5,10)
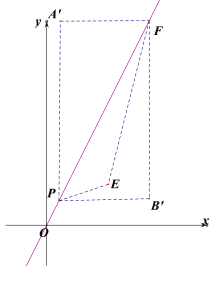
當m≤1時,作為投影矩形![]() ,如圖所示,
,如圖所示,
此時點P(m,2m),PA′=10-2m,FA′=5-m,
∴投影比k=![]() ;
;

當3≤m<5時,此時A′E=10-2=8,B′E=5-3=2,此時k=![]() .
.
綜上所述:當m≤1時,k=2;當3≤m<5時,k=4.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】把具有某種規律的一列數:1,-2,3,-4,5,-6,...,排列成下面的陣形:
 ........
........
探索下列事件:
(1)第10行的第1個數是什么數?
(2)數字2019前面是負號還是正號?在第幾行?第幾列?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,E是CB延長線上一個動點,F、G分別為AE、BC的中點,FG與ED相交于點H.
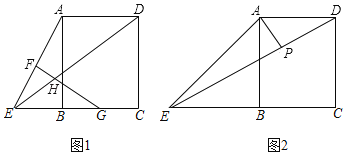
(1)求證:HE=HG;
(2)如圖2,當BE=AB時,過點A作AP⊥DE于點P,連接BP,求PQ與PB的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(發現)
(1)如圖1,在ABCD中,點O是對角線的交點,過點O的直線分別交AD,BC于點E,F.求證:△AOE≌△COF;

(探究)
(2)如圖2,在菱形ABCD中,點O是對角線的交點,過點O的直線分別交AD,BC于點E,F,若AC=4,BD=8,求四邊形ABFE的面積.
(應用)
(3)如圖3,邊長都為1的5個正方形如圖擺放,試利用無刻度的直尺,畫一條直線平分這5個正方形組成的圖形的面積.(要求:保留畫圖痕跡)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖AM∥BN,C是BN上一點, BD平分∠ABN且過AC的中點O,交AM于點D,DE⊥BD,交BN于點E.

(1)求證:△ADO≌△CBO.
(2)求證:四邊形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
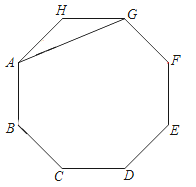
【題目】如圖,AG是正八邊形ABCDEFGH的一條對角線.
(1)在剩余的頂點B、C、D、E、F、H中,連接兩個頂點,使連接的線段與AG平行,并說明理由;
(2)兩邊延長AB、CD、EF、GH,使延長線分別交于點P、Q、M、N,若AB=2,求四邊形PQMN的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中![]() 如圖
如圖![]() ,已知拋物線
,已知拋物線![]() ,經過點
,經過點![]() 、
、![]() .
.
(1)求此拋物線頂點C的坐標;
(2)聯結AC交y軸于點D,聯結BD、BC,過點C作![]() ,垂足為點H,拋物線對稱軸交x軸于G,聯結HG,求HG的長.
,垂足為點H,拋物線對稱軸交x軸于G,聯結HG,求HG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,求值:1+2+22+23+24+…+22015.解:設S=1+2+22+23+24+…+22015,將等式兩邊同時乘以2得:2S=2+22+23+24+…+22015+22016;將下式減去上式得2S﹣S=22016﹣1;即S=1+2+22+23+24+…+22015=22016﹣1;請你仿照此法計算:
(1)1+2+22+23+…+210
(2)1+3+32+33+34+…+3n(其中n為正整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
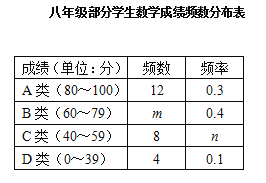
【題目】某中學八年級共有10個班,每班40名學生,學校對該年級學生數學學科某次學情調研測試成績進行了抽樣分析,請按要求回答下列問題:
(1)若要從全年級學生中抽取40人進行調查,你認為以下抽樣方法中最合理的是 .
①隨機抽取一個班級的40名學生的成績;
②在八年級學生中隨機抽取40名女學生的成績;
③在八年級10個班中每班各隨機抽取4名學生的成績.
(2)將抽取的40名學生的成績進行分組,繪制如下成績頻數分布表:
①m= ,n= ;
②根據表格中的數據,請用扇形統計圖表示學生成績分布情況.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com