
【題目】已知x,y,z均為正數.
(1)若xy<1,證明:|x+z||y+z|>4xyz;
(2)若![]() =
=![]() ,求2xy2yz2xz的最小值.
,求2xy2yz2xz的最小值.
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為菱形,四邊形ACFE為平行四邊形,設BD與AC相交于點G,AB=BD=AE=2,∠EAD=∠EAB.

(1)證明:平面ACFE⊥平面ABCD;
(2)若直線AE與BC的夾角為60°,求直線EF與平面BED所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了慶祝中華人民共和國成立70周年,某公司舉行大型抽獎活動,活動中準備了一枚質地均勻的正十二面體的骰子,在其十二個面上分別標有數字1,2,3,…,12,每位員工均有一次參與機會,并規定:若第一次拋得向上面的點數為完全平方數(即能寫成整數的平方形式,如![]() ),則立即視為獲得大獎;若第一次拋得向上面的點數不是完全平方數,則需進行第二次拋擲,兩次拋得的點數和為完全平方數(如
),則立即視為獲得大獎;若第一次拋得向上面的點數不是完全平方數,則需進行第二次拋擲,兩次拋得的點數和為完全平方數(如![]() ),也可視為獲得大獎.否則,只能獲得安慰獎.
),也可視為獲得大獎.否則,只能獲得安慰獎.
(1)試列舉須拋擲兩次才能獲得大獎的所有可能情況(用![]() 表示前后兩次拋得的點數),并說明所有可能情況的總數;
表示前后兩次拋得的點數),并說明所有可能情況的總數;
(2)若獲得大獎的獎金(單位:元)為拋得的點數或點數和(完全平方數)的360倍,而安慰獎的獎金為48元,該公司某位員工獲得的獎金為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,AC=![]() BC,AB=2BC,D為線段AB上一點,且AD=3DB,PD⊥平面ABC,PA與平面ABC所成的角為45°.
BC,AB=2BC,D為線段AB上一點,且AD=3DB,PD⊥平面ABC,PA與平面ABC所成的角為45°.
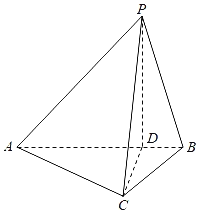
(1)求證:平面PAB⊥平面PCD;
(2)求二面角P﹣AC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在我們的教材必修一中有這樣一個問題,假設你有一筆資金,現有三種投資方案供你選擇,這三種方案的回報如下:
方案一:每天回報![]() 元;
元;
方案二:第一天回報![]() 元,以后每天比前一天多回報
元,以后每天比前一天多回報![]() 元;
元;
方案三:第一天回報![]() 元,以后每天的回報比前一天翻一番.
元,以后每天的回報比前一天翻一番.
記三種方案第![]() 天的回報分別為
天的回報分別為![]() ,
,![]() ,
,![]() .
.
(1)根據數列的定義判斷數列![]() ,
,![]() ,
,![]() 的類型,并據此寫出三個數列的通項公式;
的類型,并據此寫出三個數列的通項公式;
(2)小王準備做一個為期十天的短期投資,他應該選擇哪一種投資方案?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有下列四個結論,其中所有正確結論的編號是___________.
①若![]() ,則
,則![]() 的最大值為
的最大值為![]() ;
;
②若![]() ,
,![]() ,
,![]() 是等差數列
是等差數列![]() 的前
的前![]() 項,則
項,則![]() ;
;
③“![]() ”的一個必要不充分條件是“
”的一個必要不充分條件是“![]() ”;
”;
④“![]() ,
,![]() ”的否定為“
”的否定為“![]() ,
,![]() ”.
”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com