
【題目】某食品公司研發生產一種新的零售食品,從產品中抽取200件作為樣本,測量這些產品的一項質量指標值,由測量結果得到如下的頻率分布直方圖:
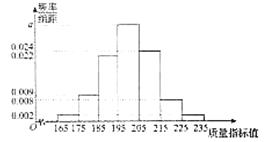
(1)求直方圖中![]() 的值;
的值;
(2)由頻率分布直方圖可認為,這種產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,試計算這批產品中質量指標值落在
,試計算這批產品中質量指標值落在![]() 上的件數;
上的件數;
(3)設產品的生產成本為![]() ,質量指標值為
,質量指標值為![]() ,生產成本與質量指標值滿足函數關系式
,生產成本與質量指標值滿足函數關系式![]() ,假設同組中的每個數據用該組數據區間的右端點代替,試計算生產該食品的平均成本.參考數據:若
,假設同組中的每個數據用該組數據區間的右端點代替,試計算生產該食品的平均成本.參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
【答案】(1)0.033;(2)68;(3)84.52
【解析】
(1)根據頻率之和為1,由頻率分布直方圖中的數據,得到結果.
(2)根據樣本容量和方差,求出正態分布中![]() 的概率,得到
的概率,得到![]() 的概率,再乘以樣本容量,得到所求件數.
的概率,再乘以樣本容量,得到所求件數.
(3)由頻率分布直方圖得到產品的成本分組及其頻率分布表,再計算出其平均成本.
(1)由頻率分布直方圖可得![]() ,
,
解得![]() .
.
(2)由于![]() ,則
,則![]() ,
,![]() ,所以
,所以![]() ,于是
,于是![]() ,
,![]() .
.
又因為![]() ,所以
,所以![]() ,于是
,于是![]() .
.
故這批產品中質量指標值落在![]() 上的件數大約為
上的件數大約為![]() .
.
(3)由頻率分布直方圖和題設條件可得產品的成本分組及其頻率分布表如下:
組號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
分組 |
|
|
|
|
|
|
|
頻率 | 0.02 | 0.09 | 0.22 | 0.33 | 0.24 | 0.08 | 0.02 |
根據題意,生產該食品的平均成本:
![]()
![]() .
.


科目:高中數學 來源: 題型:
【題目】“工資條里顯紅利,個稅新政入民心”.隨著2019年新年鐘聲的敲響,我國自1980年以來,力度最大的一次個人所得稅(簡稱個稅)改革迎來了全面實施的階段.某![]() 從業者為了解自己在個稅新政下能享受多少稅收紅利,繪制了他在26歲-35歲(2009年-2018年)之間各年的月平均收入
從業者為了解自己在個稅新政下能享受多少稅收紅利,繪制了他在26歲-35歲(2009年-2018年)之間各年的月平均收入![]() (單位:千元)的散點圖:(注:年齡代碼1-10分別對應年齡26-35歲)
(單位:千元)的散點圖:(注:年齡代碼1-10分別對應年齡26-35歲)
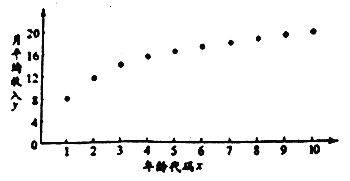
(1)由散點圖知,可用回歸模型![]() 擬合
擬合![]() 與
與![]() 的關系,試根據有關數據建立
的關系,試根據有關數據建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)如果該![]() 從業者在個稅新政下的專項附加扣除為3000元/月,試利用(1)的結果,將月平均收入視為月收入,根據新舊個稅政策,估計他36歲時每個月少繳納的個人所得稅.
從業者在個稅新政下的專項附加扣除為3000元/月,試利用(1)的結果,將月平均收入視為月收入,根據新舊個稅政策,估計他36歲時每個月少繳納的個人所得稅.
附注:①參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②參考公式:回歸方程![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為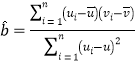 ,
,![]() .
.
③新舊個稅政策下每月應納稅所得額(含稅)計算方法及稅率表如下:
舊個稅稅率表(個稅起征點3500元) | 新個稅稅率表(個稅起征點5000元) | |||
繳稅 級數 | 每月應納稅所得額(含稅) | 稅率 | 每月應納稅所得額(含稅) | 稅率 |
1 | 不超過1500元的都分 | 3 | 不超過3000元的都分 | 3 |
2 | 超過1500元至4500元的部分 | 10 | 超過3000元至12000元的部分 | 10 |
3 | 超過4500元至9000元的部分 | 20 | 超過12000元至25000元的部分 | 20 |
4 | 超過9000元至35000元的部分 | 25 | 超過25000元至35000元的部分 | 25 |
5 | 超過35000元至55000元的部分 | 30 | 超過35000元至55000元的部分 | 30 |
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列推理不屬于合情推理的是( )
A. 由銅、鐵、鋁、金、銀等金屬能導電,得出一切金屬都能導電.
B. 半徑為![]() 的圓面積
的圓面積![]() ,則單位圓面積為
,則單位圓面積為![]() .
.
C. 由平面三角形的性質推測空間三棱錐的性質.
D. 猜想數列2,4,8,…的通項公式為![]() .
. ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列推理不屬于合情推理的是( )
A. 由銅、鐵、鋁、金、銀等金屬能導電,得出一切金屬都能導電.
B. 半徑為![]() 的圓面積
的圓面積![]() ,則單位圓面積為
,則單位圓面積為![]() .
.
C. 由平面三角形的性質推測空間三棱錐的性質.
D. 猜想數列2,4,8,…的通項公式為![]() .
. ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 的面積為
的面積為![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是
是![]() 上的兩個動點,
上的兩個動點,![]() ,試問:是否存在定點
,試問:是否存在定點![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如表是某位同學連續5次周考的數學、物理的成績,結果如下:
周次 | 1 | 2 | 3 | 4 | 5 |
數學( | 79 | 81 | 83 | 85 | 87 |
物理( | 77 | 79 | 79 | 82 | 83 |
參考公式: ,
,![]() ,
,![]() 表示樣本均值.
表示樣本均值.
(1)求該生5次月考數學成績的平均分和物理成績的方差;
(2)一般來說,學生的數學成績與物理成績有較強的線性相關關系,根據上表提供的數據,求兩個變量![]() 的線性回歸方程.
的線性回歸方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某省高三男生身高情況,現從某校高三年級男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于157.5cm和187.5cm之間,將測量結果按如下方式分成6組:第一組![]() ,第二組
,第二組![]() ,…,第六組
,…,第六組![]() ,下圖是按照上述分組方法得到的頻率分布直方圖.
,下圖是按照上述分組方法得到的頻率分布直方圖.
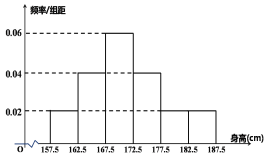
(1)求該學校高三年級男生的平均身高;
(2)利用分層抽樣的方式從這50名男生中抽出20人,求抽出的這20人中,身高在177.5cm以上(含177.5cm)的人數;
(3)從根據(2)選出的身高在177.5cm以上(含177.5cm)的男生中任意抽取2人,求此二人來自于不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P—ABC中,PA=3,PB=PC=![]() ,AB=AC=2,BC=
,AB=AC=2,BC=![]() .
.
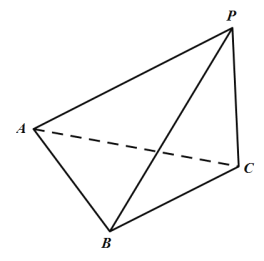
(1)求二面角B—AP—C大小的余弦值;
(2)求點P到底面ABC的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com