
【題目】已知函數![]()
(1)若![]() ,函數
,函數![]() 的極大值為
的極大值為![]() ,求實數
,求實數![]() 的值;
的值;
(2)若對任意的![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)第(1)問,先求導,對a分類討論,求出每一種情況下的極大值,得到a的方程,即可求出實數a的值. (2)第(2)問,令![]() ,轉化成證明g(a)的最大值小于等于
,轉化成證明g(a)的最大值小于等于![]() 在
在![]() 上恒成立,再分離參數
上恒成立,再分離參數![]() 對
對![]() 恒成立
恒成立![]() ,再利用導數求右邊函數的最大值得解.
,再利用導數求右邊函數的最大值得解.
試題解析:
(1)∵![]() ,
,
∴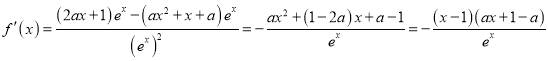
①當![]() 時,
時, ![]() ,
,
令![]() ,得
,得![]() ;
; ![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() 上單調遞減.
上單調遞減.
所以![]() 的極大值為
的極大值為![]() ,不合題意.
,不合題意.
②當![]() 時,
時, ![]() ,
,
令![]() ,得
,得![]() ;
; ![]() ,得
,得![]() 或
或![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() 和
和![]() 上單調遞減.
上單調遞減.
所以![]() 的極大值為
的極大值為![]() ,解得
,解得![]() .符合題意.
.符合題意.
綜上可得![]() .
.
(2)令![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上是增函數
上是增函數
則![]() 對
對![]() 恒成立等價于
恒成立等價于![]() ,
,
即![]() 對
對![]() 恒成立.
恒成立.
即![]() 對
對![]() 恒成立
恒成立![]()
令![]()
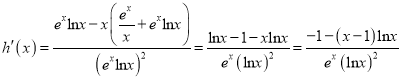
![]()
![]()
![]()
![]() 在
在![]() 上單調遞減。
上單調遞減。![]()
![]()
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】某公司擬購買一塊地皮建休閑公園,如圖,從公園入口![]() 沿
沿![]() ,
,![]() 方向修建兩條小路,休息亭
方向修建兩條小路,休息亭![]() 與入口的距離為
與入口的距離為![]() 米(其中
米(其中![]() 為正常數),過
為正常數),過![]() 修建一條筆直的鵝卵石健身步行帶,步行帶交兩條小路于
修建一條筆直的鵝卵石健身步行帶,步行帶交兩條小路于![]() 、
、![]() 處,已知
處,已知![]() ,
,![]() .
.

(1)設![]() 米,
米,![]() 米,求
米,求![]() 關于
關于![]() 的函數關系式及定義域;
的函數關系式及定義域;
(2)試確定![]() ,
,![]() 的位置,使三條路圍成的三角形
的位置,使三條路圍成的三角形![]() 地皮購價最低.
地皮購價最低.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是正方體的平面展開圖,在這個正方體中,有以下四個命題:①![]() 平面ADNE;②
平面ADNE;②![]() 平面ABFE;③平面
平面ABFE;③平面![]() 平面AFN;④平面
平面AFN;④平面![]() 平面NCF.其中正確命題的序號是( )
平面NCF.其中正確命題的序號是( )
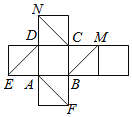
A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的準線與
的準線與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 作圓
作圓![]() 的兩條切線,切點為
的兩條切線,切點為![]() ,且
,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 是過定點
是過定點![]() 的一條直線,且與拋物線
的一條直線,且與拋物線![]() 交于
交于![]() 兩點,過定點
兩點,過定點![]() 作
作![]() 的垂線與拋物線交于
的垂線與拋物線交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(13分)設{an}是公比為正數的等比數列a1=2,a3=a2+4.
(Ⅰ)求{an}的通項公式;
(Ⅱ)設{bn}是首項為1,公差為2的等差數列,求數列{an+bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
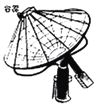
【題目】如圖是一種加熱食物的太陽灶,上面裝有可旋轉的拋物面形的反光鏡,鏡的軸截面是拋物線的一部分,盛食物的容器放在拋物線的焦點處,容器由若干根等長的鐵筋焊接在一起的架子支撐.已知鏡口圓的直徑為8m,鏡深1m.
(1)建立適當的坐標系,求拋物線的方程和焦點的位置;
(2)若把盛水和食物的容器近似地看作點,試求每根鐵筋的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列![]() 的前n項和為
的前n項和為![]() ,對于任意的
,對于任意的![]() ,都有
,都有![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求數列![]() 的通項公式;
的通項公式;
(3)令![]() 問是否存在正數m,使得
問是否存在正數m,使得![]() 對一切正整數n都成立?若存在,求出m的取值范圍;若不存在,請說明理由.
對一切正整數n都成立?若存在,求出m的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站退出了關于生態文明建設進展情況的調查,調查數據表明,環境治理和保護問題仍是百姓最為關心的熱點,參與調查者中關注此問題的約占![]() .現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組
.現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
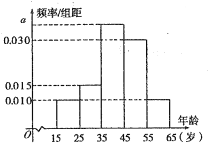
(1)求出![]() 的值;
的值;
(2)求這200人年齡的樣本平均數(同一組數據用該區間的中點值作代表)和中位數(精確到小數點后一位);
(3)現在要從年齡較小的第1,2組中用分層抽樣的方法抽取5人,再從這5人中隨機抽取3人進行問卷調查,求這2組恰好抽到2人的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com