日本.亚洲电影,久久字幕精品一区,亚洲欧美日本精品

精英家教網 > 高中數學 > 題目詳情

【題目】（1）求直線在矩陣對應變換作用下的直線的方程；

（2）在平面直角坐標系中，已知曲線以原點為極點，軸正半軸為極軸建立極坐標系，直線的極坐標方程為，求曲線C與直線交點的極坐標.

【答案】（1）；（2）.

【解析】

（1）設直線上任意一點，在矩陣M對應變換作用下的點，然后矩陣的變換列出關系式，代入原直線方程即可求出變換后的直線.

（2）將曲線C和直線方程轉化為直角坐標系下的直角坐標方程，求出交點坐標，然后再轉化為極坐標即可.

（1）設直線上任意一點，在矩陣M對應變換作用下的點

則，所以，解得.

因為點在直線上，

所以，即，

所以變換后的直線的方程為.

（2）已知曲線（α為參數），

轉換為直角坐標方程為：，

直線的極坐標方程為．

轉換為直角坐標方程為：.

由，解得：或

轉換為極坐標為.

練習冊系列答案

好學生小學口算題卡系列答案

遠航教育口算題卡系列答案

揚帆文化100分培優智能優選卷系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】一兒童游樂場擬建造一個“蛋筒”型游樂設施，其軸截面如圖中實線所示．ABCD是等腰梯形，AB=20米，∠CBF=α（F在AB的延長線上，α為銳角）．圓E與AD，BC都相切，且其半徑長為100﹣80sinα米．EO是垂直于AB的一個立柱，則當sinα的值設計為多少時，立柱EO最矮？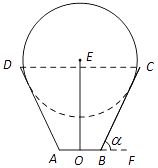

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】2015年12月10日, 我國科學家屠呦呦教授由于在發現青蒿素和治療瘧疾的療法上的貢獻獲得諾貝爾醫學獎，以青蒿素類藥物為主的聯合療法已經成為世界衛生組織推薦的抗瘧疾標準療法，目前，國內青蒿人工種植發展迅速，調查表明，人工種植的青蒿的長勢與海拔高度、土壤酸堿度、空氣濕度的指標有極強的相關性，現將這三項的指標分別記為，并對它們進行量化：0表示不合格，1表示臨界合格，2表示合格，再用綜合指標的值評定人工種植的青蒿的長勢等級：若，則長勢為一級；若，則長勢為二級；若，則長勢為三級；為了了解目前人工種植的青蒿的長勢情況，研究人員隨機抽取了10塊青蒿人工種植地，得到如下結果：

種植地編號

種植地編號

（1）在這10塊青蒿人工種植地中任取兩地，求這兩地的空氣濕度的指標相同的概率；

（2）從長勢等級是一級的人工種植地中任取一地，其綜合指標為，從長勢等級不是一級的人工種植地中任取一地，其綜合指標為，記隨機變量，求的分布列及其數學期望.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】(2016·重慶高二檢測)如圖，三棱柱ABC-A1B1C1中，側棱垂直底面，∠ACB=90°，AC=BC=AA1，D是棱AA1的中點.

(1)證明：平面BDC1⊥平面BDC.

(2)平面BDC1分此棱柱為兩部分，求這兩部分體積的比.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某教育主管部門到一所中學檢查學生的體質健康情況．從全體學生中，隨機抽取12名進行體質健康測試，測試成績（百分制）以莖葉圖形式表示如圖所示．根據學生體質健康標準，成績不低于76的為優良．

（1）寫出這組數據的眾數和中位數；
（2）將頻率視為概率．根據樣本估計總體的思想，在該校學生中任選3人進行體質健康測試，求至少有1人成績是“優良”的概率；
（3）從抽取的12人中隨機選取3人，記ξ表示成績“優良”的學生人數，求ξ的分布列及期望．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】大型綜藝節目《最強大腦》中，有一個游戲叫做盲擰魔方，就是玩家先觀察魔方狀態并進行記憶，記住后蒙住眼睛快速還原魔方，盲擰在外人看來很神奇，其實原理是十分簡單的，要學會盲擰也是很容易的.根據調查顯示，是否喜歡盲擰魔方與性別有關.為了驗證這個結論，某興趣小組隨機抽取了50名魔方愛好者進行調查，得到的情況如下表所示：

	喜歡盲擰	不喜歡盲擰	總計
男	22	▲	30
女	▲	12	▲
總計	▲	▲	50

表1

并邀請這30名男生參加盲擰三階魔方比賽，其完成情況如下表所示：

成功完成時間（分鐘）	[0，10)	[10，20)	[20，30)	[30，40]
人數	10	10	5	5

表2

（1）將表1補充完整，并判斷能否在犯錯誤的概率不超過0.025的前提下認為是否喜歡盲擰與性別有關？

（2）根據表2中的數據，求這30名男生成功完成盲擰的平均時間（同一組中的數據用該組區間的中點值代替）；

（3）現從表2中成功完成時間在[0，10)內的10名男生中任意抽取3人對他們的盲擰情況進行視頻記錄，記成功完成時間在[0，10)內的甲、乙、丙3人中被抽到的人數為，求的分布列及數學期望.

附參考公式及數據：，其中.

	0.10	0.05	0.025	0.010	0.005	0.001
	2.706	3.841	5.024	6.635	7.879	10.828

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知橢圓C：（a＞b＞0）的焦距為4，其短軸的兩個端點與長軸的一個端點構成正三角形．
（1）求橢圓C的標準方程；
（2）設F為橢圓C的左焦點，M為直線x=﹣3上任意一點，過F作MF的垂線交橢圓C于點P，Q．證明：OM經過線段PQ的中點N．（其中O為坐標原點）

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某商場舉行促銷活動，有兩個摸獎箱，箱內有一個“”號球，兩個“”號球，三個“”號球、四個無號球，箱內有五個“”號球，五個“”號球，每次摸獎后放回，每位顧客消費額滿元有一次箱內摸獎機會，消費額滿元有一次箱內摸獎機會，摸得有數字的球則中獎，“”號球獎元，“”號球獎元，“”號球獎元，摸得無號球則沒有獎金。