
【題目】三棱錐P ABC中,PA⊥平面ABC,![]() Q是BC邊上的一個動點,且直線PQ與面ABC所成角的最大值為
Q是BC邊上的一個動點,且直線PQ與面ABC所成角的最大值為![]() 則該三棱錐外接球的表面積為( )
則該三棱錐外接球的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根據題意畫出圖形,結合圖形找出△ABC的外接圓圓心與三棱錐P﹣ABC外接球的球心,
求出外接球的半徑,再計算它的表面積.
三棱錐P﹣ABC中,PA⊥平面ABC,直線PQ與平面ABC所成角為θ,
如圖所示;則sinθ=![]() =
=![]() ,且sinθ的最大值是
,且sinθ的最大值是![]() ,
,
∴(PQ)min=2![]() ,∴AQ的最小值是
,∴AQ的最小值是![]() ,即A到BC的距離為
,即A到BC的距離為![]() ,
,
∴AQ⊥BC,∵AB=2![]() ,在Rt△ABQ中可得
,在Rt△ABQ中可得![]() ,即可得BC=6;
,即可得BC=6;
取△ABC的外接圓圓心為O′,作OO′∥PA,
∴![]() =2r,解得r=2
=2r,解得r=2![]() ;
;
∴O′A=2![]() ,
,
取H為PA的中點,∴OH=O′A=2![]() ,PH=
,PH=![]() ,
,
由勾股定理得OP=R=![]() =
=![]() ,
,
∴三棱錐P﹣ABC的外接球的表面積是
S=4πR2=4×![]() =57π.
=57π.
故答案為:C


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,
,![]() ,
,![]() ,
,![]() 是其左右頂點,點
是其左右頂點,點![]() 是橢圓
是橢圓![]() 上任一點,且
上任一點,且![]() 的周長為6,若
的周長為6,若![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若過點![]() 且斜率不為0的直線交橢圓
且斜率不為0的直線交橢圓![]() 于
于![]() ,
,![]() 兩個不同點,證明:直線
兩個不同點,證明:直線![]() 與
與![]() 的交點在一條定直線上.
的交點在一條定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,直線![]() 將矩形紙
將矩形紙![]() 分為兩個直角梯形
分為兩個直角梯形![]() 和
和![]() ,將梯形
,將梯形![]() 沿邊
沿邊![]() 翻折,如圖2,在翻折的過程中(平面
翻折,如圖2,在翻折的過程中(平面![]() 和平面
和平面![]() 不重合),下面說法正確的是
不重合),下面說法正確的是
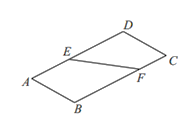
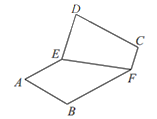
圖1 圖2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的過程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的過程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,(
,(![]() ).
).
(1)若曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,求實數am的值;
,求實數am的值;
(2)關于x的方程![]() 能否有三個不同的實根?證明你的結論;
能否有三個不同的實根?證明你的結論;
(3)若![]() 對任意
對任意![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐PABCD的底面ABCD是矩形,PA⊥底面ABCD,點E、F分別是棱PC、PD的中點,則
①棱AB與PD所在直線垂直;
②平面PBC與平面ABCD垂直;
③△PCD的面積大于△PAB的面積;
④直線AE與直線BF是異面直線.
以上結論正確的是________.(寫出所有正確結論的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:
滿足:![]() ,且對任意
,且對任意![]() ,
,![]() (s,k,l,
(s,k,l,![]() )都有
)都有![]() ,則稱數列
,則稱數列![]() 為“T”數列.
為“T”數列.
(1)證明:正項無窮等差數列![]() 是“T”數列;
是“T”數列;
(2)記正項等比數列![]() 的前n項之和為
的前n項之和為![]() ,若數列
,若數列![]() 是“T”數列,求數列
是“T”數列,求數列![]() 公比的取值范圍;
公比的取值范圍;
(3)若數列![]() 是“T”數列,且數列
是“T”數列,且數列![]() 的前n項之和
的前n項之和![]() 滿足
滿足![]() ,求證:數列
,求證:數列![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型公司為了切實保障員工的健康安全,貫徹好衛生防疫工作的相關要求,決定在全公司范圍內舉行一次![]() 普查,為此需要抽驗1000人的血樣進行化驗,由于人數較多,檢疫部門制定了下列兩種可供選擇的方案.方案①:將每個人的血分別化驗,這時需要驗1000次.方案②:按
普查,為此需要抽驗1000人的血樣進行化驗,由于人數較多,檢疫部門制定了下列兩種可供選擇的方案.方案①:將每個人的血分別化驗,這時需要驗1000次.方案②:按![]() 個人一組進行隨機分組,把從每組
個人一組進行隨機分組,把從每組![]() 個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這
個人抽來的血混合在一起進行檢驗,如果每個人的血均為陰性,則驗出的結果呈陰性,這![]() 個人的血只需檢驗一次(這時認為每個人的血化驗
個人的血只需檢驗一次(這時認為每個人的血化驗![]() 次);否則,若呈陽性,則需對這
次);否則,若呈陽性,則需對這![]() 個人的血樣再分別進行一次化驗,這樣,該組
個人的血樣再分別進行一次化驗,這樣,該組![]() 個人的血總共需要化驗
個人的血總共需要化驗![]() 次.假設此次普查中每個人的血樣化驗呈陽性的概率為
次.假設此次普查中每個人的血樣化驗呈陽性的概率為![]() ,且這些人之間的試驗反應相互獨立.
,且這些人之間的試驗反應相互獨立.
(1)設方案②中,某組![]() 個人的每個人的血化驗次數為
個人的每個人的血化驗次數為![]() ,求
,求![]() 的分布列;
的分布列;
(2)設![]() ,試比較方案②中,分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案①,化驗次數最多可以平均減少多少次?(最后結果四舍五入保留整數)
,試比較方案②中,分別取2,3,4時,各需化驗的平均總次數;并指出在這三種分組情況下,相比方案①,化驗次數最多可以平均減少多少次?(最后結果四舍五入保留整數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,長為3的線段的兩端點
中,長為3的線段的兩端點![]() 分別在
分別在![]() 軸、
軸、![]() 軸上滑動,點
軸上滑動,點![]() 為線段
為線段![]() 上的點,且滿足
上的點,且滿足![]() .記點
.記點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若點![]() 為曲線
為曲線![]() 上的兩個動點,記
上的兩個動點,記![]() ,判斷是否存在常數
,判斷是否存在常數![]() 使得點
使得點![]() 到直線
到直線![]() 的距離為定值?若存在,求出常數
的距離為定值?若存在,求出常數![]() 的值和這個定值;若不存在,請說明理由.
的值和這個定值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com