
【題目】如圖,橢圓W:![]() 的焦距與橢圓Ω:
的焦距與橢圓Ω:![]() +y2=1的短軸長相等,且W與Ω的長軸長相等,這兩個橢圓的在第一象限的交點為A,直線l經過Ω在y軸正半軸上的頂點B且與直線OA(O為坐標原點)垂直,l與Ω的另一個交點為C,l與W交于M,N兩點.
+y2=1的短軸長相等,且W與Ω的長軸長相等,這兩個橢圓的在第一象限的交點為A,直線l經過Ω在y軸正半軸上的頂點B且與直線OA(O為坐標原點)垂直,l與Ω的另一個交點為C,l與W交于M,N兩點.
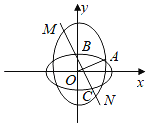
(1)求W的標準方程:
(2)求![]() .
.
科目:高中數學 來源: 題型:
【題目】一些選手參加數學競賽,其中有些選手互相認識,有些選手互相不認識,而任何兩個不相識的選手都恰有兩個共同的熟人.若![]() 與
與![]() 認識,但沒有共同的熟人,求證:
認識,但沒有共同的熟人,求證:![]() 、
、![]() 認識的熟人一樣多.
認識的熟人一樣多.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (a>b>0)的兩個焦點分別為F1,F2,離心率為
(a>b>0)的兩個焦點分別為F1,F2,離心率為![]() ,過F1的直線l與橢圓C交于M,N兩點,且△MNF2的周長為8.
,過F1的直線l與橢圓C交于M,N兩點,且△MNF2的周長為8.
(1)求橢圓C的方程;
(2)若直線y=kx+b與橢圓C分別交于A,B兩點,且OA⊥OB,試問點O到直線AB的距離是否為定值,證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小店每天以每份5元的價格從食品廠購進若干份食品,然后以每份10元的價格出售.如果當天賣不完,剩下的食品還可以每份1元的價格退回食品廠處理.
(Ⅰ)若小店一天購進16份,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() (單位:份,
(單位:份,![]() )的函數解析式;
)的函數解析式;
(Ⅱ)小店記錄了100天這種食品的日需求量(單位:份),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天記錄的各需求量的頻率作為各需求量發生的概率.
(i)小店一天購進16份這種食品,![]() 表示當天的利潤(單位:元),求
表示當天的利潤(單位:元),求![]() 的分布列及數學期望;
的分布列及數學期望;
(ii)以小店當天利潤的期望值為決策依據,你認為一天應購進食品16份還是17份?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】試確定平面上是否存在滿足下述條件的兩個不相交的無限點集![]() 、
、![]() :
:
(1)在![]() 中,任何三點不共線,且任何兩點的距離至少為1;
中,任何三點不共線,且任何兩點的距離至少為1;
(2)任何一個頂點在![]() 中的三角形,其內部均存在一個
中的三角形,其內部均存在一個![]() 中的點,任何一個頂點在
中的點,任何一個頂點在![]() 中的三角形,其內部均存在一個
中的三角形,其內部均存在一個![]() 中的點.
中的點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 是定義在
是定義在![]() 上的偶函數,且對任意的
上的偶函數,且對任意的![]() 恒有
恒有![]() ,已知當
,已知當![]() 時,
時,![]() ,則
,則
①![]() 是函數
是函數![]() 的一個周期;
的一個周期;
②函數![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數;
上是增函數;
③函數![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() ;
;
④![]() 是函數
是函數![]() 的一個對稱軸;
的一個對稱軸;
其中所有正確命題的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設![]() 為
為![]() 內一點,直線
內一點,直線![]() 、
、![]() 、
、![]() 與邊
與邊![]() 、
、![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() 、
、![]() .設分別以
.設分別以![]() 、
、![]() 為直徑的兩圓交于點
為直徑的兩圓交于點![]() 、
、![]() ,分別以
,分別以![]() 、
、![]() 為直徑的兩圓交于點
為直徑的兩圓交于點![]() 、
、![]() ,分別以
,分別以![]() 、
、![]() 為直徑的兩圓交于點
為直徑的兩圓交于點![]() 、
、![]() .證明:
.證明:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六點共圓.
六點共圓.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com