【題目】如圖，設(shè)
為
內(nèi)一點，直線
、
、
與邊
、
、
分別交于點
、
、
．設(shè)分別以、
為直徑的兩圓交于點
、
，分別以、
為直徑的兩圓交于點
、
，分別以、
為直徑的兩圓交于點
、
．證明：、、、、、六點共圓．
【答案】見解析
【解析】
首先證明：
、
、
三線共點于
，其中，為
的垂心．
如圖，作
于點
，
于點
，
于點
．
則
、
、
共點于，即的垂心．
由，知以
、
為直徑的圓均過點、
．故
為兩圓根軸．
類似地，以
、為直徑的圓均過點、
，為兩圓根軸；以、為直徑的圓均過點
、
，為兩圓根軸．
由根心定理，知、、三線共點，且與交于點．
故過點．
由、、、四點共圓
．
類似地，、均過點，有
，
．
又
，故、、
、
四點共圓于
，、、
、
四點共圓于
，、、、四點共圓于
．
如圖，設(shè)
、、
的中點分別為
、
、
，、
、
的中點分別為
、
、
．
其次證明：
、
、
三線共點．
因為
，
，所以，為的中垂線．
類似地，為的中垂線，為的中垂線．
故
為與的交點，
為與的交點，
為與的交點．
又、、共點于
，由塞瓦定理得
．
再由塞瓦定理的逆定理，知、、三線共點．
因此，、、三點重合．
故、、、、、六點共圓．
桃李文化快樂暑假武漢出版社系列答案科目：高中數(shù)學 來源： 題型：
【題目】如圖，橢圓W：
的焦距與橢圓Ω：
+y2＝1的短軸長相等，且W與Ω的長軸長相等，這兩個橢圓的在第一象限的交點為A，直線l經(jīng)過Ω在y軸正半軸上的頂點B且與直線OA（O為坐標原點）垂直，l與Ω的另一個交點為C，l與W交于M，N兩點．
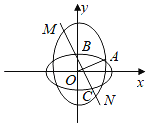
（1）求W的標準方程：
（2）求
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，其最小正周期為 
．
（1）求 
的表達式；
（2）將函數(shù)的圖象向右平移
個單位長度后，再將得到的圖象上各點的橫坐標伸長到原來的
倍（縱坐標不變），得到函數(shù) 
的圖象，若關(guān)于 
的方程 
在區(qū)間 
上有解，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某校實行選科走班制度，張毅同學的選擇是物理、生物、政治這三科，且物理在A層班級，生物在B層班級，該校周一上午課程安排如表所示，張毅選擇三個科目的課各上一節(jié)，另外一節(jié)上自習，則他不同的選課方法有（ ）
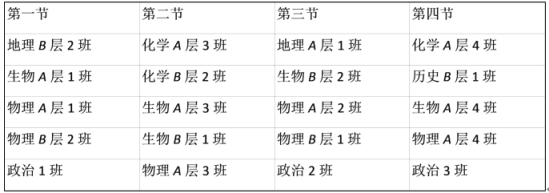
A.8種B.10種C.12種D.14種
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f(x)＝x2＋2aln x.
(1)當a＝1時，求函數(shù)f′(x)的最小值；
(2)求函數(shù)f(x)的單調(diào)區(qū)間和極值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
在
處取得極值．
（Ⅰ）求函數(shù)
的解析式；
（Ⅱ）求證：對于區(qū)間
上任意兩個自變量的值
，都有
；
（Ⅲ）若過點
可作曲線
的三條切線，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】給定函數(shù)①
;②
;③
；④
，其中在區(qū)間
上單調(diào)遞減的函數(shù)序號是( )
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】[2019·開封一模]已知數(shù)列
中，
，
，利用下面程序框圖計算該數(shù)列的項時，若輸出的是2，則判斷框內(nèi)的條件不可能是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
