
【題目】已知函數![]() 是奇函數.
是奇函數.
(1)求a的值和函數f(x)的定義域;
(2)解不等式f(-m2+2m-1)+f(m2+3)<0.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)根據函數奇偶性的定義建立方程即可求出a,根據分式函數的意義即可求出函數的定義域.
(2)根據函數奇偶性和單調性的性質將不等式進行轉化求解即可.
詳解:
(1)因為函數f(x)=![]() +a是奇函數,所以f(-x)=-f(x),
+a是奇函數,所以f(-x)=-f(x),
即![]() +a=
+a=![]() -a,即
-a,即![]() =
=![]() ,從而有1-a=a,解得a=
,從而有1-a=a,解得a=![]() .
.
又2x-1≠0,所以x≠0,故函數f(x)的定義域為(-∞,0)∪(0,+∞).
(2)由f(-m2+2m-1)+f(m2+3)<0,得f(-m2+2m-1)<-f(m2+3),因為函數f(x)為奇函數,所以f(-m2+2m-1)<f(-m2-3).
由(1)可知函數f(x)在(0,+∞)上是減函數,從而在(-∞,0)上是減函數,又-m2+2m-1<0,-m2-3<0,所以-m2+2m-1>-m2-3,且![]() 解得m>-1,且
解得m>-1,且![]() ,所以不等式的解集為
,所以不等式的解集為![]()


科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,若關于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8個不同的實數根,則b+c的取值范圍為( )
,若關于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8個不同的實數根,則b+c的取值范圍為( )
A.(﹣∞,3)
B.(0,3]
C.[0,3]
D.(0,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的短軸長為2,離心率e=
=1(a>b>0)的短軸長為2,離心率e= ![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若直線l:y=kx+m與橢圓交于不同的兩點A,B,與圓x2+y2= ![]() 相切于點M.
相切于點M.
(i)證明:OA⊥OB(O為坐標原點);
(ii)設λ= ![]() ,求實數λ的取值范圍.
,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等差數列,Sn為{an}的前n項和,且a10=19,S10=100;數列{bn}對任意n∈N* , 總有b1b2b3…bn﹣1bn=an+2成立.
(Ⅰ)求數列{an}和{bn}的通項公式;
(Ⅱ)記cn=(﹣1)n ![]() ,求數列{cn}的前n項和Tn .
,求數列{cn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,⊙O是以AB為直徑的圓,點C在圓上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延長線與AB的延長線交于點E.若EB=6,EC=6 ![]() ,則BC的長為 .
,則BC的長為 . 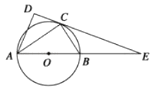
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有4個人去參加某娛樂活動,該活動有甲、乙兩個游戲可供參加者選擇.為增加趣味性,約定:每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲,擲出點數為1或2的人去參加甲游戲,擲出點數大于2的人去參加乙游戲.
(Ⅰ)求這4個人中恰有2人去參加甲游戲的概率;
(Ⅱ)用X,Y分別表示這4個人中去參加甲、乙游戲的人數,記ξ=|X﹣Y|,求隨機變量ξ的分布列與數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() ﹣…+
﹣…+ ![]() ﹣
﹣ ![]() +
+ ![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A.f(x)在(0,1)上恰有一個零點
B.f(x)在(0,1)上恰有兩個零點
C.f(x)在(﹣1,0)上恰有一個零點
D.f(x)在(﹣1,0)上恰有兩個零點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com