
已知函數
 的圖像過坐標原點
的圖像過坐標原點 ,且在點
,且在點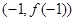 處的切線的斜率是
處的切線的斜率是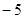 .
.
(1)求實數 的值;
的值;
(2)求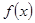 在區間
在區間 上的最大值;
上的最大值;
(3)對任意給定的正實數 ,曲線
,曲線 上是否存在兩點
上是否存在兩點 ,使得
,使得 是以
是以 為直角頂點的直角三角形,且此三角形斜邊的中點在
為直角頂點的直角三角形,且此三角形斜邊的中點在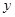 軸上?請說明理由.
軸上?請說明理由.
(1)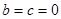 ;(2)
;(2) 在
在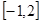 上的最大值為
上的最大值為 ;(3)對任意給定的正實數
;(3)對任意給定的正實數 ,曲線
,曲線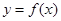 上總存在兩點
上總存在兩點 ,使得
,使得 是以
是以 為直角頂點的直角三角形,且此三角形斜邊的中點在y軸上.
為直角頂點的直角三角形,且此三角形斜邊的中點在y軸上.
解析試題分析:(1)求實數 的值,由函數
的值,由函數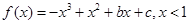 ,由圖像過坐標原點
,由圖像過坐標原點 ,得
,得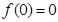 ,且根據函數在點
,且根據函數在點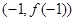 處的切線的斜率是
處的切線的斜率是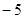 ,由導數幾何意義可得
,由導數幾何意義可得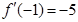 ,建立方程組,可確定實數
,建立方程組,可確定實數 的值,進而可確定函數的解析式;(2)求
的值,進而可確定函數的解析式;(2)求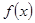 在區間
在區間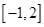 的最大值,因為
的最大值,因為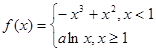 ,由于
,由于 是分段函數,可分段求最大值,最后確定最大值,當
是分段函數,可分段求最大值,最后確定最大值,當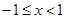 時,
時,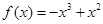 ,求導得,
,求導得, ,令
,令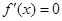 ,可得
,可得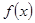 在
在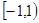 上的最大值為
上的最大值為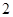 ,當
,當 時,
時, .對
.對 討論,確定函數的單調性,即可求得結論;(3)這是探索性命題,可假設曲線
討論,確定函數的單調性,即可求得結論;(3)這是探索性命題,可假設曲線 上存在兩點
上存在兩點 滿足題設要求,則點
滿足題設要求,則點 只能在
只能在 軸兩側.設
軸兩側.設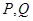 的坐標,由此入手能得到對任意給定的正實數
的坐標,由此入手能得到對任意給定的正實數 ,曲線
,曲線 上存在兩點
上存在兩點 使得
使得 是以
是以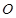 為直角頂點的直角三角形,且此三角形斜邊中點在
為直角頂點的直角三角形,且此三角形斜邊中點在 軸上.
軸上.
試題解析:(1)當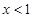 時,
時,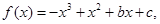 則
則 (1分)
(1分)
依題意,得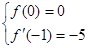 即
即 ,解得
,解得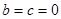 . (3分)
. (3分)
(2)由(1)知,
 ①當
①當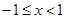 時
時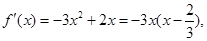 令
令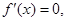 得
得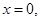 或
或 (4分)
(4分)
當 變化時
變化時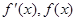 的變化情況如下表:
的變化情況如下表: