
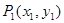 ,
,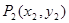 ,…,
,…, ,…是曲線
,…是曲線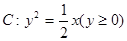 上的點,
上的點,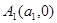 ,
, ,…,
,…, ,…是
,…是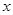 軸正半軸上的點,且
軸正半軸上的點,且 ,
,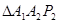 ,…,
,…, ,… 均為斜邊在
,… 均為斜邊在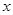 軸上的等腰直角三角形(
軸上的等腰直角三角形( 為坐標原點).
為坐標原點). 、
、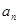 和
和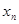 之間的等量關系,以及
之間的等量關系,以及 、
、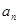 和
和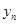 之間的等量關系;
之間的等量關系; (
(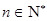 );
);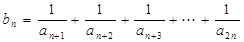 ,對所有
,對所有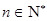 ,
,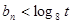 恒成立,求實數
恒成立,求實數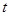 的取值范圍.
的取值范圍.
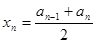 ,
,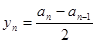 (2)
(2)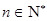 ,
, (3)
(3)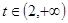
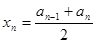 ,
,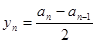 得到
得到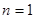 時,可求得
時,可求得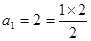 ,命題成立;②假設當
,命題成立;②假設當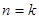 時,命題成立,即有
時,命題成立,即有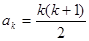 則當
則當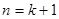 時,由歸納假設及
時,由歸納假設及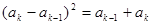 ,
,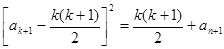
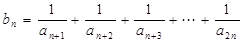
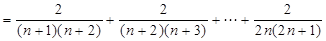
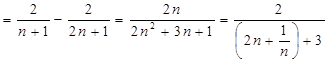 .………………………2分
.………………………2分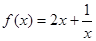 在區間
在區間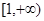 上單調遞增,所以當
上單調遞增,所以當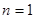 時,
時,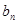 最大為
最大為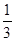 ,即
,即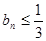
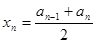 ,
,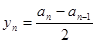 ,………………4分
,………………4分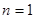 時,可求得
時,可求得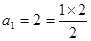 ,命題成立; ……………2分
,命題成立; ……………2分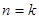 時,命題成立,即有
時,命題成立,即有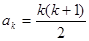 ,……………………1分
,……………………1分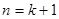 時,由歸納假設及
時,由歸納假設及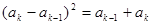 ,
,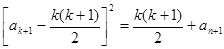 .
.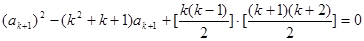
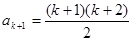 (
(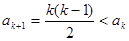 不合題意,舍去)
不合題意,舍去)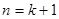 時,命題成立. …………………………………………4分
時,命題成立. …………………………………………4分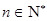 ,
, . ……………………………1分
. ……………………………1分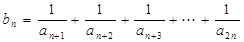
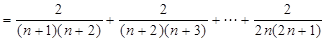
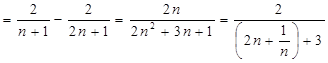 .………………………2分
.………………………2分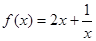 在區間
在區間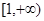 上單調遞增,所以當
上單調遞增,所以當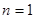 時,
時,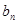 最大為
最大為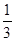 ,即
,即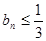 .……………2分
.……………2分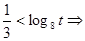
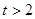 . 所以,
. 所以,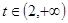


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com