【題目】甲居住在城鎮的
處,準備開車到單位
處上班,若該地各路段發生堵車事件都是相互獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率如圖(例如：
算作兩個路段：路段
發生堵車事件的概率為
,路段
發生堵車事件的概率為
).
(1)請你為甲選擇一條由到的最短路線
(即此人只選擇從西向東和從南向北的路線),
使得途中發生堵車事件的概率最小；
(2)設甲在路線
中遇到的堵車次數為隨機變量,求的數學期望
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知
是橢圓
的左、右焦點，離心率為
，
是平面內兩點，滿足
，線段
的中點
在橢圓上，
周長為12.
（1）求橢圓
的方程；
（2）若與圓
相切的直線
與橢圓交于
，求
（其中
為坐標原點）的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】算籌是在珠算發明以前我國獨創并且有效的計算工具，為我國古代數學的發展做出了很大貢獻.在算籌計數法中，以“縱式”和“橫式”兩種方式來表示數字，如圖：
表示多位數時，個位用縱式，十位用橫式，百位用縱式，千位用橫式，以此類推，遇零則置空，如圖：
如果把5根算籌以適當的方式全部放入 下面的表格中，那么可以表示的三位數的個數為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖a是某市參加2012年高考的學生身高條形統計圖，從左到右的各條形表示的學生人數依次記為
、
、…、
[如表示身高（單位：cm）在
內的學生人數]．圖b是統計圖a中身高在一定范圍內學生人數的一個算法流程圖．現要統計身高在
（含160cm，不含180cm）的學生人數，那么在流程圖中的判斷框內應填寫的條件是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱
的底面是正三角形，
底面
，M為
的中點．
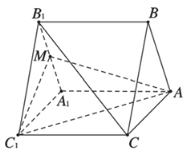
（1）求證：
平面
；
（2）若
，且沿側棱
展開三棱柱的側面，得到的側面展開圖的對角線長為
，求作點
在平面內的射影H，請說明作法和理由，并求線段AH的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
世紀中葉，中國數學家賈憲給出了直到六次冪的二項式系數表，如圖所示是《楊輝詳解九章算法》開方作法本原，其中第
層即為
展開式的系數．賈憲稱整張數表為“開放作法本原”，今稱“賈憲三角”但賈憲未給出二項式系數的一般公式，因而未能建立一般正整數次冪的二項式定理．賈憲的數學著作已失傳，
世紀數學家楊輝在《詳解九章算法》
中引用了開放作法本原圖，注明此圖出“《釋鎖算數》，賈憲用此術”，因而流傳至今．只是后人往往因此把它誤稱為“楊輝三角”．
展開式中
的系數為
，①則實數
的值為_______________，②展開式中各項系數之和為__________________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，且以橢圓
的兩焦點和短軸的一個端點為頂點的三角形的周長恰為
.
（1）求橢圓的標準方程；
（2）動直線
與拋橢圓相交于
，
兩點，問：在
軸上是否存在定點
（其中
，使得向量
與向量
共線（其中
為坐標原點）？若存在，求出點
的坐標；若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
