
已知向量a=
 ,b=
,b= ,c=
,c= ,
,
(1)求證:(a+b)⊥(a-b);
(2)設函數
 ,求
,求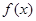 的最大值和最小值.[來
的最大值和最小值.[來
(2)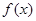 的最大值為4,最小值為0.
的最大值為4,最小值為0.
【解析】(1)計算向量的數量積;(2)將f(x)化為 4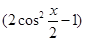 . 再由x∈
. 再由x∈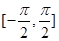 ,
得
,
得 ∈
∈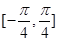 求解.
求解.
解:(1)【解法一】依題意得:a+b=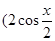 ,
,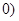 ,a-b=
,a-b=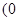 ,
,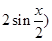
∴(a+b)·(a-b)=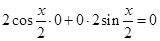 ,
,
∴(a+b)⊥(a-b). (5分)
【解法二】依題意得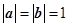 ,∴(a+b)·(a-b)=
,∴(a+b)·(a-b)=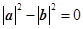 ,
,
∴(a+b)⊥(a-b). (5分)
(2)依題意得a+c=(cos +1,sin
+1,sin -1),b+c=(cos
-1),b+c=(cos +1,-sin
+1,-sin -1),
-1),
∴|a+c|2-3=(cos +1)2+(sin
+1)2+(sin -1)2-3=2cos
-1)2-3=2cos -2sin
-2sin ,
,
|b+c|2-3=(cos +1)2+(-sin
+1)2+(-sin -1)2-3=2cos
-1)2-3=2cos +2sin
+2sin ,
,
∴f(x)=(|a+c|2-3)(|b+c|2-3)=(2cos -2sin
-2sin )(2cos
)(2cos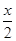 +2sin
+2sin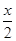 )
)
=4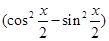 =4
=4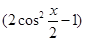 . 又x∈
. 又x∈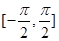 ,
∴
,
∴ ∈
∈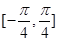
故當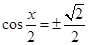 ,即
,即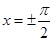 時,
時,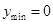 ;當
;當 ,即
,即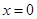 時,
時,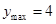
∴函數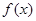 的最大值為4,最小值為0.
(12分)
的最大值為4,最小值為0.
(12分)


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:高考總復習全解 數學 一輪復習·必修課程 (人教實驗版) B版 人教實驗版 B版 題型:044
已知向量a=![]() ,b=
,b=![]() 且
且
x∈[0,![]() ],求:
],求:
(1)a·b及|a+b|;(2)若f(x)=a·b-2λ|a+b|的最小值是-![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中數學 來源:吉林省白山二中2012屆高三第二次月考數學文科試題 題型:013
已知向量a=![]() ,b=(0,-1),c=
,b=(0,-1),c=![]() .若a-2b與c共線,則k=
.若a-2b與c共線,則k=
A.1
B.![]()
C.-1
D.3
查看答案和解析>>
科目:高中數學 來源:2013-2014學年上海交大附中高三數學理總復習二三角恒等變換與解三角形練習卷(解析版) 題型:選擇題
已知向量a= ,b=(4,4cos α-
,b=(4,4cos α- ),若a⊥b,則sin
),若a⊥b,則sin 等于( )
等于( )
A.- B.-
B.-
C. D.
D.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com