【題目】已知函數
.
（1）求函數
的單調區間；
（2）當
時，如果方程
有兩個不等實根
，求實數t的取值范圍，并證明
.
【答案】（1）當
時，
的單調遞增區間是
，單調遞減區間是
；當
時，的單調遞增區間是，單調遞減區間是；（2）
，證明見解析.
【解析】
（1）求出
，對
分類討論，分別求出
的解，即可得出結論；
（2）由（1）得出
有兩解時
的范圍，以及
關系，將
，等價轉化為證明
，不妨設
，令
，則
，即證
，構造函數
，只要證明對于任意
恒成立即可.
（1）的定義域為R，且
.
由
，得
；由
，得
.
故當時，函數的單調遞增區間是，
單調遞減區間是；
當時，函數的單調遞增區間是，
單調遞減區間是.
（2）由（1）知當
時，
，且
.
當
時，
；當
時，
.
當
時，直線
與
的圖像有兩個交點，
實數t的取值范圍是.
方程有兩個不等實根
，
，
，
，
，
，即
.
要證，只需證
，
即證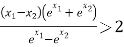
，不妨設.
令，則，
則要證
，即證.
令，則
.
令
，則
，
在
上單調遞增，
.
，
在上單調遞增，
，即
成立，
即成立.
.
開心試卷期末沖刺100分系列答案
雙基同步導航訓練系列答案科目：高中數學 來源： 題型：
【題目】已知某公司生產某產品的年固定成本為100萬元，每生產1千件需另投入27萬元，設該公司一年內生產該產品
千件
并全部銷售完，每千件的銷售收入為
萬元，且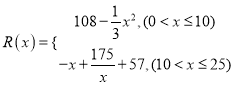
.
⑴ 寫出年利潤
（萬元）關于年產量
（千件）的函數解析式；
⑵ 當年產量為多少千件時，該公司在這一產品的生產中所獲年利潤最大？（注：年利潤＝年銷售收入
年總成本）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，以O為極點，x軸的正半軸為極軸建立極坐標系，直線l的極坐標方程為
，Q為l上的動點，以OQ為邊作等邊三角形OPQ，且三點O，P，Q按逆時針方向排列.
（Ⅰ）設點P運動軌跡E的直角坐標方程；
（Ⅱ）若曲線
經過伸縮變換
得到曲線
，若點M為曲線上的動點，且點M到曲線E的最小距離為1，求實數a的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于集合
，
，
，
，定義
.
集合
中的元素個數記為
，當
，稱集合具有性質
.
（1）已知集合
，
，寫出
，
的值，并判斷集合是否具有性質；
（2）設集合
具有性質，判斷集合
中的三個元素是否能組成等差數列，請說明理由；
（3）若數列
是以
為首項，2為公比的等比數列. 數列中的前100項：
組成的集合
記作
，將集合
中的所有元素
從小到大排序，即
滿足
，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著夏季的到來，冰枕成為市面上的一種熱銷產品，某廠家為了調查冰枕在當地大學的銷售情況，作出調研，并將所得數據統計如下表所示：
表一：
溫度在30℃以下 | 溫度在30℃以上 | 總計 | |
女生 | 10 | 30 | 40 |
男生 | 40 | 20 | 60 |
總計 | 50 | 50 | 100 |
隨后在該大學一個小賣部調查了冰枕的出售情況，并將某月的日銷售件數（x）與銷售天數（y）統計如下表所示：
表二：
第 | 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
（1）請根據表二中的數據在下列網格紙中繪制散點圖；
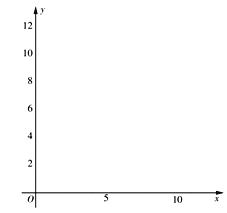
（2）請根據表二中提供的數據，用最小二乘法求出y關于x的線性回歸方程
；
（3）從（1）（2）中的數據及回歸方程我們可以得到，銷售件數隨著銷售天數的增長而增長，但無法判斷男、女生對冰枕的選擇是否與溫度有關，請結合表一中的數據，并自己設計方案來判段是否有99.9%的可能性說明購買冰枕的性別與溫度相關.
參考數據及公式：
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
；
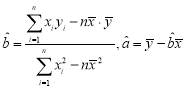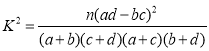，其中
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
