
【題目】已知函數(shù)![]() 的兩個零點為
的兩個零點為![]() .
.
(1)求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)求證: ![]() .
.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析: (1)方法一的思路是:求出函數(shù)![]() 的最大值,有兩個零點,再最大值一定大于零,求出實數(shù)
的最大值,有兩個零點,再最大值一定大于零,求出實數(shù)![]() 的范圍.方法二是轉(zhuǎn)化為兩個函數(shù)的圖象有兩個交點; (2)采用綜合法和分析法證明不等式.構(gòu)造函數(shù)
的范圍.方法二是轉(zhuǎn)化為兩個函數(shù)的圖象有兩個交點; (2)采用綜合法和分析法證明不等式.構(gòu)造函數(shù)![]() ,利用單調(diào)性求出
,利用單調(diào)性求出![]() 的范圍,構(gòu)造函數(shù)
的范圍,構(gòu)造函數(shù)![]() ,證明
,證明![]() 在
在![]() 上為增函數(shù),
上為增函數(shù), ![]() ,化簡,得證.
,化簡,得證.
試題解析:(1)方法一: ![]() ,
,
①![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上單調(diào)遞增,不可能有兩個零點.
上單調(diào)遞增,不可能有兩個零點.
②![]() 時,由
時,由![]() 可解得
可解得![]() ,由
,由![]() 可解得
可解得![]() .
.
∴![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,于是
上單調(diào)遞增,于是![]() .
.
要使得![]() 在
在![]() 上有兩個零點,則
上有兩個零點,則![]() ,解得
,解得![]() ,即
,即![]() 的取值范圍為
的取值范圍為![]() .
.
方法二: ![]() ,可轉(zhuǎn)化為函數(shù)
,可轉(zhuǎn)化為函數(shù)![]() 與函數(shù)
與函數(shù)![]() 圖象有兩個交點.
圖象有兩個交點.
∵![]() ,∴當(dāng)
,∴當(dāng)![]() 時,
時, ![]() ;
; ![]() 時,
時, ![]() .即
.即![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
∴![]() .
.
∴![]() ,即
,即![]() 的取值范圍為
的取值范圍為![]() .
.
(2)令![]() ,則
,則![]() ,由題意知方程
,由題意知方程![]() 有兩個根
有兩個根![]() ,即方程
,即方程![]() 有兩個根
有兩個根![]() ,不妨設(shè)
,不妨設(shè)![]() .
.
令![]() ,則
,則![]() ,由
,由![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,∴
,∴![]() 時,
時, ![]() 單調(diào)遞增,
單調(diào)遞增, ![]() 時,
時, ![]() 單調(diào)遞減.
單調(diào)遞減.
根據(jù)已知有: ![]() ,要證
,要證![]() ,即證
,即證![]() ,即
,即![]() .
.
即證![]() .令
.令![]() ,下面證
,下面證![]() 對任意的
對任意的![]() 恒成立.
恒成立.
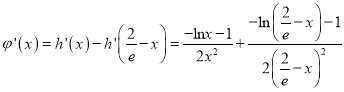 ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() .
.
∴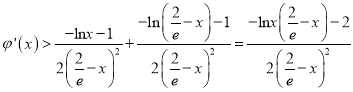 .
.
∵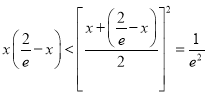 ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 是增函數(shù),∴
是增函數(shù),∴![]() ,∴
,∴![]() .
.
點睛: 本題主要考查函數(shù)的導(dǎo)數(shù)的綜合應(yīng)用,函數(shù)的單調(diào)性與零點,構(gòu)造法的應(yīng)用,考查學(xué)生分析問題解決問題的能力,難度比較大.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1) ![]() 時,證明:
時,證明: ![]() ;
;
(2)當(dāng)![]() 時,直線
時,直線![]() 和曲線
和曲線![]() 切于點
切于點![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(3)當(dāng)![]() 時,不等式
時,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a>0且a≠1,下列四組函數(shù)中表示相等函數(shù)的是( )
A.y=logax與y=(logxa)﹣1
B.y=2x與y=logaa2x
C.![]() 與y=x
與y=x
D.y=logax2與y=2logax
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司生產(chǎn)一種電子儀器的固定成本為20000元,每生產(chǎn)一臺儀器需增加投入100元,已知總收益滿足函數(shù):R(x)= 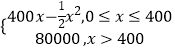 ,其中x是儀器的月產(chǎn)量.(注:總收益=總成本+利潤)
,其中x是儀器的月產(chǎn)量.(注:總收益=總成本+利潤)
(1)將利潤x表示為月產(chǎn)量x的函數(shù);
(2)當(dāng)月產(chǎn)量為何值時,公司所獲利潤最大?最大利潤為多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|2x﹣a|,g(x)=x+1.
(1)若a=1,求不等式f(x)≤1的解集;
(2)對任意的x∈R,f(x)+|g(x)|≥a2+2a(a>0)恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示的鋼板的邊界![]() 是拋物線的一部分,且
是拋物線的一部分,且![]() 垂直于拋物線對稱軸,現(xiàn)欲從鋼板上截取一塊以
垂直于拋物線對稱軸,現(xiàn)欲從鋼板上截取一塊以![]() 為下底邊的等腰梯形鋼板
為下底邊的等腰梯形鋼板![]() ,其中
,其中![]() 均在拋物線弧上.設(shè)
均在拋物線弧上.設(shè)![]() (米),且
(米),且![]() .
.
(1)當(dāng)![]() 時,求等腰梯形鋼板的面積;
時,求等腰梯形鋼板的面積;
(2)當(dāng)![]() 為何值時,等腰梯形鋼板的面積最大?并求出最大值.
為何值時,等腰梯形鋼板的面積最大?并求出最大值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如果集合A,B,同時滿足A∪B={1,2,3,4},A∩B={1},A≠{1},B≠{1},就稱有序集對(A,B)為“好集對”.這里有序集對(A,B)意指,當(dāng)A≠B時,(A,B)和(B,A)是不同的集對,那么“好集對”一共有( )個.
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一企業(yè)從某條生產(chǎn)線上隨機(jī)抽取30件產(chǎn)品,測量這些產(chǎn)品的某項技術(shù)指標(biāo)值![]() ,得到如下的頻數(shù)分布表:
,得到如下的頻數(shù)分布表:
|
|
|
|
|
頻數(shù) | 2 | 6 | 18 | 4 |
(I)估計該技術(shù)指標(biāo)值的平均數(shù);(用各組區(qū)間中點值作代表)
(II) 若![]() 或
或![]() ,則該產(chǎn)品不合格,其余的是合格產(chǎn)品,試估計該條生產(chǎn)線生產(chǎn)的產(chǎn)品為合格品的概率;
,則該產(chǎn)品不合格,其余的是合格產(chǎn)品,試估計該條生產(chǎn)線生產(chǎn)的產(chǎn)品為合格品的概率;
(III)生產(chǎn)一件產(chǎn)品,若是合格品可盈利80元,不合格品則虧損10元,在(II)的前提下,從該生產(chǎn)線生產(chǎn)的產(chǎn)品中任取出兩件,記![]() 為兩件產(chǎn)品的總利潤,求隨機(jī)變量X的分布列和期望.
為兩件產(chǎn)品的總利潤,求隨機(jī)變量X的分布列和期望.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com