
【題目】已知向量a=![]() ,b=
,b=![]() ,且x∈
,且x∈![]() .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值是-![]() ,求λ的值.
,求λ的值.
【答案】見解析
【解析】解 (1)a·b=cos ![]() cos
cos ![]() -sin
-sin ![]() sin
sin ![]() =cos 2x,
=cos 2x,
|a+b|=![]()
=![]() =2
=2![]() ,
,
因為x∈![]() ,所以cos x≥0,
,所以cos x≥0,
所以|a+b|=2cos x.
(2)由(1),可得f(x)=a·b-2λ|a+b|=cos 2x-4λcos x,
即f(x)=2(cos x-λ)2-1-2λ2.
因為x∈![]() ,所以0≤cos x≤1.
,所以0≤cos x≤1.
①當λ<0時,當且僅當cos x=0時,f(x)取得最小值-1,這與已知矛盾;
②當0≤λ≤1時,當且僅當cos x=λ時,f(x)取得最小值-1-2λ2,由已知得-1-2λ2=-![]() ,解得λ=
,解得λ=![]() ;
;
③當λ>1時,當且僅當cos x=1時,f(x)取得最小值1-4λ,由已知得1-4λ=-![]() ,解得λ=
,解得λ=![]() ,這與λ>1相矛盾;綜上所述λ=
,這與λ>1相矛盾;綜上所述λ=![]() .
.


科目:高中數學 來源: 題型:
【題目】隨著人口老齡化的到來,我國的勞動力人口在不斷減少,“延遲退休”已經成為人們越來越關心的話題,為了解公眾對“延遲退休”的態度,某校課外研究性學習小組在某社區隨機抽取了50人進行調查,將調查情況進行整理后制成下表:
年齡 |
|
|
|
|
|
人數 | 4 | 5 | 8 | 5 | 3 |
年齡 |
|
|
|
|
|
人數 | 6 | 7 | 3 | 5 | 4 |
經調查年齡在![]() ,
,![]() 的被調查者中贊成“延遲退休”的人數分別是3人和2人,現從這兩組的被調查者中各隨機選取2人,進行跟蹤調查.
的被調查者中贊成“延遲退休”的人數分別是3人和2人,現從這兩組的被調查者中各隨機選取2人,進行跟蹤調查.
(Ⅰ)求年齡在![]() 的被調查者中選取的2人都贊成“延遲退休”的概率;
的被調查者中選取的2人都贊成“延遲退休”的概率;
(Ⅱ)若選中的4人中,不贊成“延遲退休”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1)所示,E為矩形ABCD的邊AD上一點,動點P、Q同時從點B出發,點P以1cm/秒的速度沿折線BE-ED-DC運動到點C時停止,點Q以2cm/秒的速度沿BC運動到點C時停止.設P、Q同時出發t秒時,△BPQ的面積為ycm2.已知y與t的函數關系圖象如圖(2)(其中曲線OG為拋物線的一部分,其余各部分均為線段),則下列結論:①![]() ;②當
;②當![]() 時,
時, ![]() ;③
;③![]() ;④當
;④當![]() 秒時,
秒時, ![]() ∽
∽![]() ;⑤當
;⑤當![]() 的面積為
的面積為![]() 時,時間
時,時間![]() 的值是
的值是![]() 或
或![]() ;其中正確的結論是( )
;其中正確的結論是( )
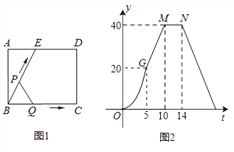
A. ①⑤ B. ②⑤ C. ②③ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
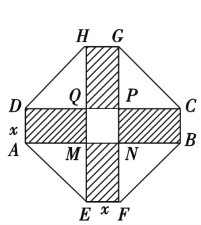
【題目】某居民小區要建造一座八邊形的休閑小區,它的主體造型的平面圖是由兩個相同的矩形ABCD和EFGH構成的,是面積為200平方米的十字形地帶.計劃在正方MNPQ上建一座花壇,造價是每平方米4 200元,在四個相同的矩形(圖中陰影部分)上鋪上花崗巖地坪,造價是每平方米210元,再在四個空角上鋪上草坪,造價是每平方米80元.
(1)設總造價是S元,AD長為x米,試建立S關于x的函數關系式;
(2)當x為何值時,S最小?并求出最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種電子儀器的固定成本為20 000元,每生產一臺儀器需增加投入100元,已知總收益滿足函數:
R(x)=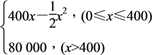
其中x是儀器的月產量.
(1)將利潤表示為月產量的函數f(x);
(2)當月產量為何值時,公司所獲得利潤最大?最大利潤為多少元?(總收益=總成本+利潤)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐P-ABCD的底面ABCD是正方形,E,F分別為AC和PB上的點,它的直觀圖,正視圖,側視圖如圖所示.
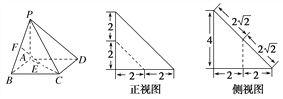
(1)求EF與平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com