Question

【題目】已知橢圓C1的方程為 + =1，雙曲線C2的左、右焦點分別是C1的左、右頂點，而以雙曲線C2的左、右頂點分別是橢圓C1的左、右焦點．
（1）求雙曲線C2的方程；
（2）記O為坐標原點，過點Q（0，2）的直線l與雙曲線C2相交于不同的兩點E、F，若△OEF的面積為2 ，求直線l的方程．

Answer 1

【答案】
（1）解：設雙曲線C2的方程： ，

則c2=4，a2=4﹣2=2，由a2+b2=c2，則b2=2，

故雙曲線C2的方程：

（2）解：由題意可知：設直線l的方程y=kx+2，則 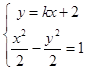，整理得：（1﹣k2）x2﹣4kx﹣6=0，

直線l與雙曲線相交于不同兩點E，F，

則 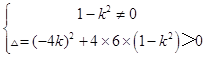，解得﹣ ＜k＜﹣1或1＜k＜ ，

設E（x1，y1），F（x2，y1），則x1+x2= ，x1x2= ，

則丨EF丨= = ，

原點O到直線l的距離d= ，

則△OEF的面積S= ×d×丨EF丨= × × = ，

由S=2 ，則 =2 ，整理得：k4﹣k2﹣2=0，

解得：k= ，

滿足﹣ ＜k＜﹣1或1＜k＜ ，

故滿足條件的直線l有兩條，其方程為y= x+2或y=﹣ x+2

【解析】（1）設雙曲線的方程，由雙曲線的性質，即可求得a和b的方程，即可求得雙曲線的方程；（2）設直線l的方程，代入雙曲線方程，利用韋達定理及弦長公式即可求得丨EF丨，利用三角形的面積公式，即可求得k的值，求得直線l的方程．