【題目】數(shù)列
的前
項和記為
， 
，點
在直線
上， 
．
（1）求數(shù)列
的通項公式；
（2）設(shè)
， 
， 
是數(shù)列
的前
項和，求
．
【答案】（1）
；（2）
.
【解析】試題分析：（1）由
在直線
上可得， 
，所以
，兩式相減得
為等比數(shù)列，從而得出
的通項公式；（2）求出
，利用分組求和法以及等差數(shù)列的求和公式與等比數(shù)列的求和公式可得出
.
試題解析：（1）由題知
，所以
，兩式相減得
，又
，
所以
是以1為首項，4為公比的等比數(shù)列．
（2）
， 
，
所以
.
【方法點晴】本題主要考查等比數(shù)列的定義與通項、等差數(shù)列的求和公式與等比數(shù)列的求和公式以及利用“分組求和法”求數(shù)列前
項和，屬于中檔題. 利用“分組求和法”求數(shù)列前
項和常見類型有兩種：一是通項為兩個公比不相等的等比數(shù)列的和或差，可以分別用等比數(shù)列求和后再相加減；二是通項為一個等差數(shù)列和一個等比數(shù)列的和或差，可以分別用等差數(shù)列求和、等比數(shù)列求和后再相加減.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在每年的3月份，濮陽市政府都會發(fā)動市民參與到植樹綠化活動中去林業(yè)管理部門為了保證樹苗的質(zhì)量都會在植樹前對樹苗進行檢測，現(xiàn)從甲、乙兩種樹苗中各抽測了
株樹苗，量出它們的高度如下(單位：厘米)，
甲：37，21，31，20，29，19，32，23，25，33；
乙：10，30，47，27，46，14，26，10，44，46.
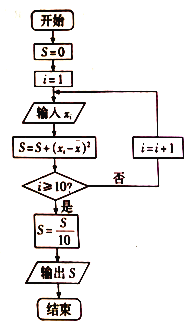
（1）畫出兩組數(shù)據(jù)的莖葉圖并根據(jù)莖葉圖對甲、乙兩種樹苗的高度作比較，寫出兩個統(tǒng)計結(jié)論；
（2）設(shè)抽測的株甲種樹苗高度平均值為
，將這株樹苗的高度依次輸人，按程序框(如圖)進行運算，問輸出的
大小為多少?并說明的統(tǒng)計學(xué)意義，
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在四棱錐
中，平面
平面
，側(cè)面
是邊長為
的等邊三角形，底面
是矩形，且
，則該四棱錐外接球的表面積等于__________.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線C：y2=2px過點P（1，1）.過點（0， 
）作直線l與拋物線C交于不同的兩點M，N，過點M作x軸的垂線分別與直線OP，ON交于點A，B，其中O為原點.
（Ⅰ）求拋物線C的方程，并求其焦點坐標(biāo)和準(zhǔn)線方程；
（Ⅱ）求證：A為線段BM的中點.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】圓x2＋y2－2y－1＝0關(guān)于直線y＝x對稱的圓的方程是 ( )
A. (x－1)2＋y2＝2 B. (x＋1)2＋y2＝2 C. (x－1)2＋y2＝4 D. (x＋1)2＋y2＝4
【答案】A
【解析】圓
的標(biāo)準(zhǔn)方程為
，所以圓心為（0,1），半徑為
，圓心關(guān)于直線
的對稱點是（1,0），所以圓x2＋y2－2y－1＝0關(guān)于直線y＝x對稱的圓的方程是
，選A.
點睛：本題主要考查圓關(guān)于直線的對稱的圓的方程，屬于基礎(chǔ)題。解答本題的關(guān)鍵是求出圓心關(guān)于直線的對稱點，兩圓半徑相同。
【題型】單選題
【結(jié)束】
8
【題目】已知雙曲線的離心率為
，焦點是
， 
，則雙曲線方程為 （ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】數(shù)列
的前
項和記為
， 
，點
在直線
上， 
．
（1）求數(shù)列
的通項公式；
（2）設(shè)
， 
， 
是數(shù)列
的前
項和，求
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】齊王與田忌賽馬，田忌的上等馬優(yōu)于齊王的中等馬，劣于齊王的上等馬，田忌的中等馬優(yōu)于齊王的下等馬，劣于齊王的中等馬， 田忌的下等馬劣于齊王的下等馬.現(xiàn)從雙方的馬匹中隨機選一匹進行一場比賽，則田忌的馬獲勝的概率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
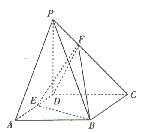
【題目】已知四棱錐
中，四邊形
是菱形， 
，又
平面
,
點
是棱
的中點， 
在棱
上，且
.
（1）證明：平面
平面
；
（2）若
平面
，求四棱錐
的體積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
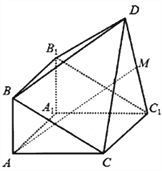
【題目】如圖，由直三棱柱
和四棱錐
構(gòu)成的幾何體中， 
，平面
平面
．
（Ⅰ）求證： 
；
（Ⅱ）在線段
上是否存在點
，使直線
與平面
所成的角為
？若存在，求
的值，若不存在，說明理由．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com