
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,點
,點![]() 是曲線
是曲線![]() 上的動點,點
上的動點,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,點
,點![]() 的軌跡為
的軌跡為![]() .
.
(1)求直線![]() 及曲線
及曲線![]() 的極坐標方程;
的極坐標方程;
(2)若射線![]() 與直線
與直線![]() 交于點
交于點![]() ,與曲線
,與曲線![]() 交于點
交于點![]() (與原點不重合),求
(與原點不重合),求![]() 的最大值.
的最大值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
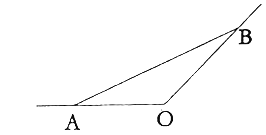
【題目】如圖所示,某城市有一條從正西方AO通過市中心O后向東北OB的公路,現要修一條地鐵L,在OA,OB上各設一站A,B,地鐵在AB部分為直線段,現要求市中心O與AB的距離為![]() ,設地鐵在AB部分的總長度為
,設地鐵在AB部分的總長度為![]() .
.
![]() 按下列要求建立關系式:
按下列要求建立關系式:
![]() 設
設![]() ,將y表示成
,將y表示成![]() 的函數;
的函數;
![]() 設
設![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B兩站分別設在公路上離中心O多遠處,才能使AB最短?并求出最短距離.
把A,B兩站分別設在公路上離中心O多遠處,才能使AB最短?并求出最短距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖①是一棟新農村別墅,它由上部屋頂和下部主體兩部分組成.如圖②,屋頂由四坡屋面構成,其中前后兩坡屋面ABFE和CDEF是全等的等腰梯形,左右兩坡屋面EAD和FBC是全等的三角形.點F在平面ABCD和BC上的射影分別為H,M.已知HM 5 m,BC 10 m,梯形ABFE的面積是△FBC面積的2.2倍.設∠FMH ![]()
![]() .
.
(1)求屋頂面積S關于![]() 的函數關系式;
的函數關系式;
(2)已知上部屋頂造價與屋頂面積成正比,比例系數為k(k為正的常數),下部主體造價與其 高度成正比,比例系數為16 k.現欲造一棟上、下總高度為6 m的別墅,試問:當![]() 為何值時,總造價最低?
為何值時,總造價最低?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為 為參數
為參數![]() ,以坐標原點為極點,x軸的正半軸為極軸建建立極坐標系,曲線C的極坐標方程為
,以坐標原點為極點,x軸的正半軸為極軸建建立極坐標系,曲線C的極坐標方程為![]() .
.
![]() 求曲線C的直角坐標方程與直線l的極坐標方程;
求曲線C的直角坐標方程與直線l的極坐標方程;
![]() Ⅱ
Ⅱ![]() 若直線
若直線![]() 與曲線C交于點
與曲線C交于點![]() 不同于原點
不同于原點![]() ,與直線l交于點B,求
,與直線l交于點B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在![]() 上的函數
上的函數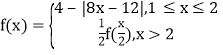 及如下的4個命題:
及如下的4個命題:
![]() 關于x的方程
關于x的方程![]() 有
有![]() 個不同的零點;
個不同的零點;
![]() 對于實數
對于實數![]() ,不等式
,不等式![]() 恒成立;
恒成立;
![]() 在
在![]() 上,方程
上,方程![]() 有5個零點;
有5個零點;
![]() 時,函數
時,函數![]() 的圖象與x軸圖成的形的面積是4.
的圖象與x軸圖成的形的面積是4.
則以上命題正確的為______![]() 把正確命題前的序號填在橫線上
把正確命題前的序號填在橫線上![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com