
���}Ŀ����D���R·![]() ��߅��һС������������
��߅��һС������������![]() �L(zh��ng)40�ף����������h(yu��n)��
�L(zh��ng)40�ף����������h(yu��n)��![]() ��
��![]() �ľ��x��400�ף��ҳ�����߅��钁�タ�ͣ��F(xi��n)Ҫ�ڳ�������߅��һ��(g��)�������εĭh(hu��n)����С·
�ľ��x��400�ף��ҳ�����߅��钁�タ�ͣ��F(xi��n)Ҫ�ڳ�������߅��һ��(g��)�������εĭh(hu��n)����С·![]() ����
����![]() ���cС�����������У�ӛ
���cС�����������У�ӛ![]() .
.

��1����С·�Ŀ��L(zh��ng)����![]() ��ʾ��
��ʾ��
��2������С·�cС����֮�g���D���Ӱ�^(q��)����ϲ�ƺ��������䁲�ƺ��e��С�r(sh��)��![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ��2����(d��ng)
��2����(d��ng)![]() �r(sh��)������䁲�ƺ��e��С
�r(sh��)������䁲�ƺ��e��С
��������
��1���������m��ƽ��ֱ������(bi��o)ϵ�����С������߅�璁�タ���̣�Ȼ���O(sh��)��ֱ��![]() �ķ��̣��͒��タ(li��n)������������c(di��n)����(bi��o)�� ͬ�r(sh��)�����
�ķ��̣��͒��タ(li��n)������������c(di��n)����(bi��o)�� ͬ�r(sh��)�����![]() ������(bi��o)����ʾ��
������(bi��o)����ʾ��![]() ��׃�μ��ɵýY(ji��)����
��׃�μ��ɵýY(ji��)����
��2��Ҫ����䁲�ƺ��e��С����Ҫ������e��С�����ã�1���ĽY(ji��)����ʾ��������e�����û�������ʽ�����ֵ��
�⣺��1����![]() ��ԭ�c(di��n)��
��ԭ�c(di��n)��![]() ����ֱ����
����ֱ����![]() �S���^�c(di��n)
�S���^�c(di��n)![]() ����ֱ��
����ֱ��![]() �S��ֱ����
�S��ֱ����![]() �S������ֱ������(bi��o)ϵ������
�S������ֱ������(bi��o)ϵ������![]() ��
��
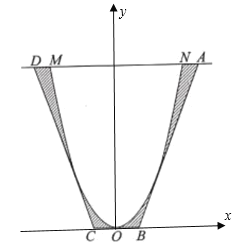
��?y��n)�С������߅��钁�タ�ͣ��O(sh��)߅�����ڵĒ��タ���̞�![]() ��
��
��?y��n)?/span>![]() ��������һ�c(di��n)��
��������һ�c(di��n)��
����![]() �������タ���̞�
�������タ���̞�![]() .
.
�O(sh��)![]() ���ڵ�ֱ�����̣�
���ڵ�ֱ�����̣�![]() ��
��
(li��n)��![]() ����
����![]() ��
��
��?y��n)?/span>![]() �c���タ���У�
�c���タ���У�
����![]() ��.
��.
ӛֱ��![]() �c���タ�����c(di��n)
�c���タ�����c(di��n)![]() ��
��
����![]() �c(di��n)�ęM����(bi��o)��
�c(di��n)�ęM����(bi��o)��![]() ����
����![]() .
.
���c(di��n)![]() ���c(di��n)
���c(di��n)![]() ���Ɍ�(du��)�Q�Կ�֪
���Ɍ�(du��)�Q�Կ�֪![]() ���c(di��n)
���c(di��n)![]() .
.
����ѷ���L(zh��ng)��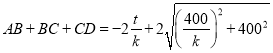 ��
��
�ɢټ�![]() ��֪
��֪
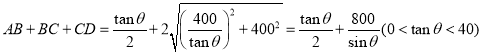 ��
��
��2��ӛ��ƺ��e��![]() ��������e��
��������e��![]() ��������e��
��������e��![]() ��
��
����![]() ����?y��n)�������e
����?y��n)�С������e![]() �鶨ֵ��Ҫʹ�ò�ƺ��e��С���t������e��С
�鶨ֵ��Ҫʹ�ò�ƺ��e��С���t������e��С
![]() ��
��
�ɢ�֪![]() ����(d��ng)�҃H��(d��ng)��
����(d��ng)�҃H��(d��ng)��![]() ��ȡ�á�����
��ȡ�á�����
���Ԯ�(d��ng)![]() �r(sh��)��������e��С������ƺ��e��С��
�r(sh��)��������e��С������ƺ��e��С��


 ͬ������(x��)���ϴ�W(xu��)������ϵ�д�
ͬ������(x��)���ϴ�W(xu��)������ϵ�д� ͬ������(x��)���ϴ�W(xu��)������ϵ�д�
ͬ������(x��)���ϴ�W(xu��)������ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
![]() ��һ�ΈD����D��ʾ.
��һ�ΈD����D��ʾ.

��1����˺���(sh��)�Ľ���ʽ��
��2����˺���(sh��)��![]() �ϵĆ��{(di��o)�f���^(q��)�g.
�ϵĆ��{(di��o)�f���^(q��)�g.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���҇��Ŵ���(sh��)�W(xu��)�������㷨�y(t��ng)�ڡ����������}�����h(yu��n)��ΡΡ���ߌӣ��t���c(di��n)�c(di��n)���������������ٰ�ʮһ��Ո(q��ng)�����^�ױK��������˼�ǣ�һ��7����������381�K�����������Ɍ��е���һ�ӟ���(sh��)����һ�ӟ���(sh��)��2�����t����플ӹ��П��� ��
A. 1�K B. 3�K C. 5�K D. 9�K
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������}�����_���ǣ�������
A.�о�?j��)ɂ�(g��)׃�����P(gu��n)�P(gu��n)ϵ�r(sh��)�����P(gu��n)ϵ��(sh��)r��ؓ(f��)��(sh��)���f���ɂ�(g��)׃������ؓ(f��)���P(gu��n)
B.�о�?j��)ɂ�(g��)׃�����P(gu��n)�P(gu��n)ϵ�r(sh��)�����P(gu��n)ָ��(sh��)R2Խ���f���ؚw���̔M��Ч��Խ�ã�
C.���}��x��R��cosx��1���ķ����}����x0��R��cosx0��1��
D.��(sh��)��(sh��)a��b��a��b������һ��(g��)��ֲ���Ҫ�l����a3��b3
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����1���O(sh��)![]() ����(sh��)��(sh��)x�M��|x��m|��2���O(sh��)
����(sh��)��(sh��)x�M��|x��m|��2���O(sh��)![]() ����(sh��)��(sh��)x�M��
����(sh��)��(sh��)x�M��![]() ��1�����Vp�ǩVq�ı�Ҫ����֗l������(sh��)��(sh��)m��ȡֵ����
��1�����Vp�ǩVq�ı�Ҫ����֗l������(sh��)��(sh��)m��ȡֵ����
��2����֪p������(sh��)f��x����ln��x2��ax+3���Ķ��x�Ǟ�R����֪q����֪![]() ��
��![]() ��ָ��(sh��)����(sh��)g��x������a��1��x�ڌ�(sh��)��(sh��)���(n��i)��p����(sh��)�����Vp��q������}����(sh��)��(sh��)a��ȡֵ������
��ָ��(sh��)����(sh��)g��x������a��1��x�ڌ�(sh��)��(sh��)���(n��i)��p����(sh��)�����Vp��q������}����(sh��)��(sh��)a��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() ��,
��,![]() ��(j��ng)�^ԭ�c(di��n)��ֱ��
��(j��ng)�^ԭ�c(di��n)��ֱ��![]() ��
��![]() �ֳ����҃ɲ���,ӛ���҃ɲ��ֵ���e�քe��
�ֳ����҃ɲ���,ӛ���҃ɲ��ֵ���e�քe��![]() ,�t
,�t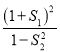 ȡ����Сֵ�r(sh��),ֱ��
ȡ����Сֵ�r(sh��),ֱ��![]() ��б�ʣ� ��
��б�ʣ� ��
A.����1B.����![]() C.����
C.����![]() D.������
D.������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�A![]() ��
��![]() �P(gu��n)��ֱ��
�P(gu��n)��ֱ��![]() ��(du��)�Q���^�c(di��n)
��(du��)�Q���^�c(di��n)![]() ��
��![]() ��ֱ��
��ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() .
.
��1���C����ֱ��![]() �c�A
�c�A![]() �ཻ��
�ཻ��
��2��ӛֱ��![]() �c�A
�c�A![]() �ăɂ�(g��)���c(di��n)��
�ăɂ�(g��)���c(di��n)��![]() ��
��![]() .
.
�������L(zh��ng)![]() ����ֱ�����̣�
����ֱ�����̣�
����![]() ��e�����ֵ��
��e�����ֵ��![]() ��e�����r(sh��)��ֱ������.
��e�����r(sh��)��ֱ������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)P�ͷ��㌍(sh��)��(sh��)![]() ����ɗl��ͬ��ֱ��
����ɗl��ͬ��ֱ��![]() ���^�c(di��n)P����б��֮�e��
���^�c(di��n)P����б��֮�e��![]() ���t�Qֱ��
���t�Qֱ��![]() ��һ�M��
��һ�M��![]() ��ܗ����(du��)������ֱ
��ܗ����(du��)������ֱ![]() ��һ�M��
��һ�M��![]() ��ܗ����(du��)��������O������(bi��o)ԭ�c(di��n).
��ܗ����(du��)��������O������(bi��o)ԭ�c(di��n).
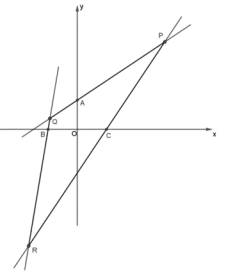
��1����֪![]() ��һ�M��
��һ�M��![]() ��ܗ����(du��)������
��ܗ����(du��)������![]() �ĊA�ǵ���Сֵ��
�ĊA�ǵ���Сֵ��
��2����֪�c(di��n)A(0,1)���c(di��n)![]() ���c(di��n)C(1,0)�քe�����lֱ��PQ,QR,RP�ϵ��c(di��n)��A,B,C�cP,Q,R�����غϣ�����ֱ��PR,PQ�ǡ�
���c(di��n)C(1,0)�քe�����lֱ��PQ,QR,RP�ϵ��c(di��n)��A,B,C�cP,Q,R�����غϣ�����ֱ��PR,PQ�ǡ�![]() ��ܗ����(du��)����ֱ��QP,QR�ǡ�
��ܗ����(du��)����ֱ��QP,QR�ǡ�![]() ��ܗ����(du��)����ֱ��RP��RQ�ǡ�
��ܗ����(du��)����ֱ��RP��RQ�ǡ�![]() ��ܗ����(du��)�������c(di��n)P������(bi��o)��
��ܗ����(du��)�������c(di��n)P������(bi��o)��
��3����֪�c(di��n)![]() ��ֱ��
��ֱ��![]() �ǡ�
�ǡ�![]() ��ܗ����(du��)������(d��ng)
��ܗ����(du��)������(d��ng)![]() ��б��׃���r(sh��)����ԭ�c(di��n)O��ֱ��
��б��׃���r(sh��)����ԭ�c(di��n)O��ֱ��![]() �ľ��x֮�e��ȡֵ����.
�ľ��x֮�e��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��![]() �У�
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() �����ģ��c(di��n)
�����ģ��c(di��n)![]() �M��
�M��![]() .
.
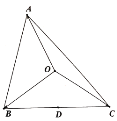
��1���C����![]() ��
��
��2����![]() ���O(sh��)
���O(sh��)![]() �c
�c![]() �ཻ���c(di��n)
�ཻ���c(di��n)![]() ��
��![]() �P(gu��n)���c(di��n)
�P(gu��n)���c(di��n)![]() ��(du��)�Q����
��(du��)�Q����![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com