
【題目】已知點P和非零實數![]() ,若兩條不同的直線
,若兩條不同的直線![]() 均過點P,且斜率之積為
均過點P,且斜率之積為![]() ,則稱直線
,則稱直線![]() 是一組“
是一組“![]() 共軛線對”,如直
共軛線對”,如直![]() 是一組“
是一組“![]() 共軛線對”,其中O是坐標原點.
共軛線對”,其中O是坐標原點.
(1)已知![]() 是一組“
是一組“![]() 共軛線對”,求
共軛線對”,求![]() 的夾角的最小值;
的夾角的最小值;
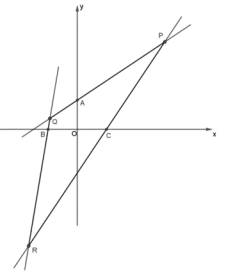
(2)已知點A(0,1)、點![]() 和點C(1,0)分別是三條直線PQ,QR,RP上的點(A,B,C與P,Q,R均不重合),且直線PR,PQ是“
和點C(1,0)分別是三條直線PQ,QR,RP上的點(A,B,C與P,Q,R均不重合),且直線PR,PQ是“![]() 共軛線對”,直線QP,QR是“
共軛線對”,直線QP,QR是“![]() 共軛線對”,直線RP,RQ是“
共軛線對”,直線RP,RQ是“![]() 共軛線對”,求點P的坐標;
共軛線對”,求點P的坐標;
(3)已知點![]() ,直線
,直線![]() 是“
是“![]() 共軛線對”,當
共軛線對”,當![]() 的斜率變化時,求原點O到直線
的斜率變化時,求原點O到直線![]() 的距離之積的取值范圍.
的距離之積的取值范圍.
【答案】(1)最小值為![]() ;(2)P(3,3)或
;(2)P(3,3)或![]() ;(3)
;(3)![]() .
.
【解析】
(1)設l1的斜率為k,則l2的斜率為![]() ,兩直線的夾角為α,利用夾角公式及基本不等式求最值,即可得到l1,l2的夾角的最小值;
,兩直線的夾角為α,利用夾角公式及基本不等式求最值,即可得到l1,l2的夾角的最小值;
(2)設直線PR,PQ,QR的斜率分別為k1,k2,k3,可得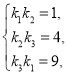 ,求解可得k1,k2,k3的值,進一步得到直線PR與直線PQ的方程,聯立得P的坐標;
,求解可得k1,k2,k3的值,進一步得到直線PR與直線PQ的方程,聯立得P的坐標;
(3)設l1:![]() ,
,![]() ,其中k≠0,利用兩點間的距離公式可得原點O到直線l1,l2的距離,變形后利用基本不等式求解.
,其中k≠0,利用兩點間的距離公式可得原點O到直線l1,l2的距離,變形后利用基本不等式求解.
(1)設![]() 的斜率為k,則
的斜率為k,則![]() 的斜率為
的斜率為![]() ,兩直線的夾角為a,
,兩直線的夾角為a,
則 ,
,
等號成立的條件是![]() ,所以最小值為
,所以最小值為![]() ;
;
(2)設直線![]() 的斜率分別為
的斜率分別為![]() ,
,
則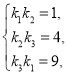 得
得![]() 或
或![]() .
.
當![]() 時,直線
時,直線![]() 的方程為y=
的方程為y=![]() ,直線
,直線![]() 的方程為y=
的方程為y=![]() ,聯立得,P(3,3);
,聯立得,P(3,3);
當![]() 時,,直線
時,,直線![]() 的方程為y=
的方程為y=![]() ,直線
,直線![]() 的方程為y=-
的方程為y=-![]() ,聯立得,
,聯立得,![]() ;
;
故所求為P(3,3)或![]() ;
;
(3)設![]() ,
,![]() ,其中k
,其中k![]() ,
,
故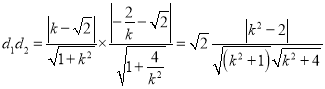 =
=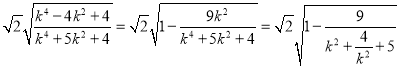
由于![]() (等號成立的條件是
(等號成立的條件是![]() ),故
),故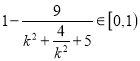 ,
,![]() .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】設函數![]() ,其中x>0,k為常數,e為自然對數的底數.
,其中x>0,k為常數,e為自然對數的底數.
(1)當k≤0時,求![]() 的單調區間;
的單調區間;
(2)若函數![]() 在區間(1,3)上存在兩個極值點,求實數k的取值范圍;
在區間(1,3)上存在兩個極值點,求實數k的取值范圍;
(3)證明:對任意給定的實數k,存在![]() (
(![]() ),使得
),使得![]() 在區間(
在區間(![]() ,
,![]() )上單調遞增.
)上單調遞增.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,馬路![]() 南邊有一小池塘,池塘岸
南邊有一小池塘,池塘岸![]() 長40米,池塘的最遠端
長40米,池塘的最遠端![]() 到
到![]() 的距離為400米,且池塘的邊界為拋物線型,現要在池塘的周邊建一個等腰梯形的環池塘小路
的距離為400米,且池塘的邊界為拋物線型,現要在池塘的周邊建一個等腰梯形的環池塘小路![]() ,且
,且![]() 均與小池塘岸線相切,記
均與小池塘岸線相切,記![]() .
.

(1)求小路的總長,用![]() 表示;
表示;
(2)若在小路與小池塘之間(圖中陰影區域)鋪上草坪,求所需鋪草坪面積最小時,![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是______.
①若直線![]() 與直線
與直線![]() 互相垂直,則
互相垂直,則![]()
②若![]() ,
,![]() 兩點到直線
兩點到直線![]() 的距離分別是
的距離分別是![]() ,
,![]() ,則滿足條件的直線
,則滿足條件的直線![]() 共有3條
共有3條
③過![]() ,
,![]() 兩點的所有直線方程可表示為
兩點的所有直線方程可表示為![]()
④經過點![]() 且在
且在![]() 軸和
軸和![]() 軸上截距都相等的直線方程為
軸上截距都相等的直線方程為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)已知等差數列{an}中,a1=1,a3=﹣3.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)若數列{an}的前k項和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩點![]() 、
、![]() ,動點
,動點![]() 滿足
滿足![]() ,記
,記![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() (
(![]() )交曲線
)交曲線![]() 于
于![]() 、
、![]() 兩點,點
兩點,點![]() 在第一象限,
在第一象限,![]() 軸,垂足為
軸,垂足為![]() ,連結
,連結![]() 并延長交曲線
并延長交曲線![]() 于點
于點![]() .
.
(1)求曲線![]() 的方程,并說明曲線
的方程,并說明曲線![]() 是什么曲線;
是什么曲線;
(2)若![]() ,求△
,求△![]() 的面積;
的面積;
(3)證明:△![]() 為直角三角形.
為直角三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產A、B兩種產品,生產每一噸產品所需的勞動力和煤、電耗如下表:
產品品種 | 勞動力 | 煤 | 電 |
A產品 | 3 | 9 | 4 |
B產品 | 10 | 4 | 5 |
已知生產每噸A產品的利潤是7萬元,生產每噸B產品的利潤是12萬元,現在條件有限,該企業僅有勞動力300個,煤360噸,并且供電局只能供電200千瓦,試問:該企業生產A、B兩種產品各多少噸,才能獲得最大利潤?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y = f(x)是定義域為R的偶函數,當x≥0時,函數f(x)的圖象是由一段拋物線和一條射線組成(如圖所示).

①當![]() 時,y的取值范圍是______;
時,y的取值范圍是______;
②如果對任意![]() (b <0),都有
(b <0),都有![]() ,那么b的最大值是______.
,那么b的最大值是______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com