
定義在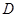 上的函數
上的函數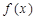 ,如果滿足:對任意
,如果滿足:對任意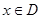 ,存在常數
,存在常數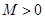 ,都有
,都有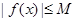 成立,則稱
成立,則稱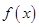 是
是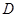 上的有界函數,其中
上的有界函數,其中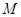 稱為函數
稱為函數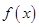 的上界.
的上界.
已知函數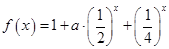 ;
;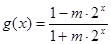 .
.
(1)當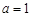 時,求函數
時,求函數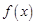 在
在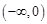 上的值域,并判斷函數
上的值域,并判斷函數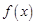 在
在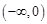 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(2)若函數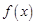 在
在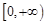 上是以3為上界的有界函數,求實數
上是以3為上界的有界函數,求實數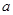 的取值范圍;
的取值范圍;
(3)若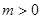 ,函數
,函數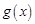 在
在 上的上界是
上的上界是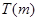 ,求
,求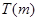 的取值范圍.
的取值范圍.
(1)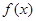 在
在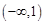 的值域為
的值域為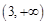 ,故不存在常數
,故不存在常數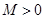 ,使
,使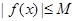 成立
成立
所以函數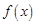 在
在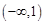 上不是有界函數。
上不是有界函數。
(2)實數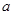 的取值范圍為
的取值范圍為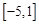 。
。
(3)當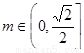 時,
時,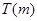 的取值范圍是
的取值范圍是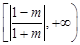 ;
;
當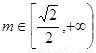 時,
時,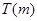 的取值范圍是
的取值范圍是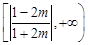
【解析】[解]:(1)當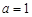 時,
時,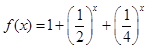
因為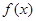 在
在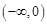 上遞減,所以
上遞減,所以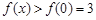 ,即
,即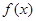 在
在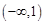 的值域為
的值域為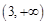
故不存在常數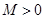 ,使
,使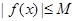 成立
成立
所以函數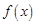 在
在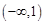 上不是有界函數。 ……………4分(沒有判斷過程,扣2分)
上不是有界函數。 ……………4分(沒有判斷過程,扣2分)
(2)由題意知,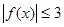 在
在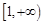 上恒成立。………5分
上恒成立。………5分
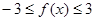 ,
, 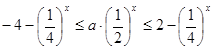
∴ 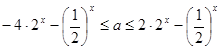 在
在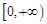 上恒成立………6分
上恒成立………6分
∴ 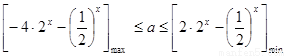 ………7分
………7分
設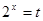 ,
,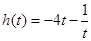 ,
,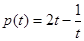 ,由
,由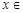
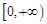 得 t≥1,
得 t≥1,
設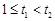 ,
,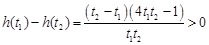
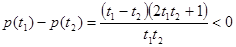
所以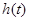 在
在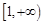 上遞減,
上遞減,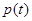 在
在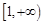 上遞增,………9分(單調性不證,不扣分)
上遞增,………9分(單調性不證,不扣分)
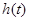 在
在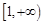 上的最大值為
上的最大值為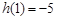 ,
, 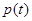 在
在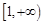 上的最小值為
上的最小值為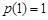
所以實數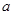 的取值范圍為
的取值范圍為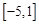 。…………………………………11分
。…………………………………11分
(3)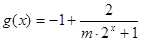 ,∵ m>0 ,
,∵ m>0 ,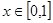 ∴
∴ 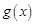 在
在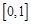 上遞減,…12分
上遞減,…12分
∴ 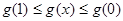 即
即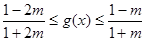 ………13分
………13分
①當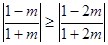 ,即
,即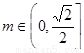 時,
時, , ………14分
, ………14分
此時 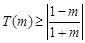 ,………16分②當
,………16分②當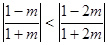 ,即
,即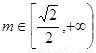 時,
時,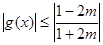 ,
,
此時  , ---------17分
, ---------17分
綜上所述,當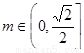 時,
時,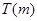 的取值范圍是
的取值范圍是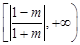 ;
;
當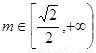 時,
時,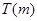 的取值范圍是
的取值范圍是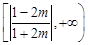 ………18分
………18分


科目:高中數學 來源:2015屆四川成都七中實驗學校高一3月月考數學試卷(解析版) 題型:選擇題
定義在 上的函數
上的函數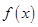 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列 ,
, 仍是等比數列,則稱
仍是等比數列,則稱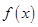 為“保等比數列函數”. 現有定義在
為“保等比數列函數”. 現有定義在 上的如下函數:
上的如下函數:
①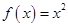 ②
② ③
③ ④
④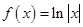
則其中是“保等比數列函數”的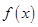 的序號為( )
的序號為( )
A.①② B.③④ C.①③ D.②④
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省東莞市高三第三次月考理科數學試卷(解析版) 題型:選擇題
定義在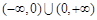 上的函數
上的函數 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列 ,
, 仍是等比數列,則稱
仍是等比數列,則稱 為“保等比數列函數”. 現有定義在
為“保等比數列函數”. 現有定義在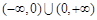 上的如下函數:
上的如下函數:
① ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
則其中是“保等比數列函數”的 的序號為( )
的序號為( )
A.① ② B.③ ④ C.① ③ D.② ④
查看答案和解析>>
科目:高中數學 來源:2012年全國普通高等學校招生統一考試理科數學(湖北卷解析版) 題型:選擇題
定義在 上的函數
上的函數 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列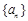 ,
,  仍是等比數列,則稱
仍是等比數列,則稱 為“保等比數列函數”. 現有定義在
為“保等比數列函數”. 現有定義在 上的如下函數:①
上的如下函數:① ; ②
; ② ; ③
; ③ ; ④
; ④ .則其中是“保等比數列函數”的
.則其中是“保等比數列函數”的 的序號為
的序號為
A、① ② B、③ ④ C、① ③ D、② ④
查看答案和解析>>
科目:高中數學 來源:2012年全國普通高等學校招生統一考試文科數學(湖北卷解析版) 題型:選擇題
定義在 上的函數
上的函數 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列 仍是等比數列,則稱
仍是等比數列,則稱 為“保等比數列函數”。現有定義在
為“保等比數列函數”。現有定義在 上的如下函數:①
上的如下函數:① ;②
;② ;③
;③ ;④
;④ 。則其中是“保等比數列函數”的
。則其中是“保等比數列函數”的 的序號為
的序號為
A、①② B、③④ C、①③ D、②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com