
【題目】已知直線![]() :
:![]() 和圓
和圓![]() :
:![]() .
.
(1)求證:直線![]() 恒過一定點
恒過一定點![]() ;
;
(2)試求當![]() 為何值時,直線
為何值時,直線![]() 被圓
被圓![]() 所截得的弦長最短;
所截得的弦長最短;
(3)在(2)的前提下,直線![]() 是過點
是過點![]() ,且與直線
,且與直線![]() 平行的直線,求圓心在直線
平行的直線,求圓心在直線![]() 上,且與圓
上,且與圓![]() 相外切的動圓中半徑最小圓的標準方程.
相外切的動圓中半徑最小圓的標準方程.
【答案】(1)![]() ; (2)
; (2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)通過直線l轉化為直線系,求出直線恒過的定點;
(2)當直線![]() 與
與![]() 垂直時,所截得的弦長最短,此時有
垂直時,所截得的弦長最短,此時有![]()
![]() =-1,由此能出m的值;
=-1,由此能出m的值;
(3)由(2)得直線![]() 的方程為
的方程為![]() ,可判斷出直線
,可判斷出直線![]() 與圓
與圓![]() 相離,設動圓圓心為
相離,設動圓圓心為![]() ,當圓心
,當圓心![]() 到圓心
到圓心![]() 的距離最小時,動圓
的距離最小時,動圓![]() 的半徑最小,從而得到最小圓的標準方程.
的半徑最小,從而得到最小圓的標準方程.
(1)證明:直線![]() 的方程可化為:
的方程可化為:![]() .
.
解方程組![]() ,得
,得![]() .
.
所以,直線![]() 恒過定點
恒過定點![]() .
.
(2)解:圓![]() :
:![]() 的標準方程為
的標準方程為![]() ,
,
表示以![]() 為圓心,
為圓心,![]() 為半徑的圓,
為半徑的圓,
![]() ,
,![]() ,
,
∴![]() 在圓
在圓![]() 內,那么對任意
內,那么對任意![]() 都有直線
都有直線![]() 與圓
與圓![]() 相交.
相交.
當直線![]() 與
與![]() 垂直時,所截弦長最短.
垂直時,所截弦長最短.
又直線![]() 的斜率
的斜率![]() ,∴此時直線
,∴此時直線![]() 的斜率為
的斜率為![]() .
.
即![]() ,解得
,解得![]() .
.
(3)解:由(2)得直線![]() 的斜率為
的斜率為![]() ,又∵
,又∵![]() ,
,
∴直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
又圓心![]() 到直線
到直線![]() 的距離
的距離![]() ,所以直線
,所以直線![]() 與圓
與圓![]() 相離.
相離.
設動圓圓心為![]() ,當圓心
,當圓心![]() 到圓心
到圓心![]() 的距離最小時,動圓
的距離最小時,動圓![]() 的半徑最小,
的半徑最小,
此時圓心![]() 為過點
為過點![]() 且與
且與![]() 垂直的直線與
垂直的直線與![]() 的交點,且動圓半徑的最小值為
的交點,且動圓半徑的最小值為![]() .
.
又過點![]() 與
與![]() 垂直的直線方程為
垂直的直線方程為![]() ,即
,即![]() .
.
解方程組![]() ,得
,得![]() .
.
即圓心![]() 為
為![]() .
.
∴所求圓的標準方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 的方程為
的方程為![]() ,
,![]() 點的坐標為
點的坐標為![]() .
.
(1)求過點![]() 且與圓
且與圓![]() 相切的直線方程;
相切的直線方程;
(2)過點![]() 任作一條直線
任作一條直線![]() 與圓
與圓![]() 交于不同兩點
交于不同兩點![]() ,
,![]() ,且圓
,且圓![]() 交
交![]() 軸正半軸于點
軸正半軸于點![]() ,求證:直線
,求證:直線![]() 與
與![]() 的斜率之和為定值.
的斜率之和為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《城市規劃管理意見》里面提出“新建住宅要推廣街區制,原則上不再建設封閉住宅小區,已建成的封閉小區和單位大院要逐步打開”,這個消息在網上一石激起千層浪,各種說法不一而足.某網站為了解居民對“開放小區”認同與否,從![]() 歲的人群中隨機抽取了
歲的人群中隨機抽取了![]() 人進行問卷調查,并且做出了各個年齡段的頻率分布直方圖(部分)如圖所示,同時對
人進行問卷調查,并且做出了各個年齡段的頻率分布直方圖(部分)如圖所示,同時對![]() 人對這“開放小區”認同情況進行統計得到下表:
人對這“開放小區”認同情況進行統計得到下表:
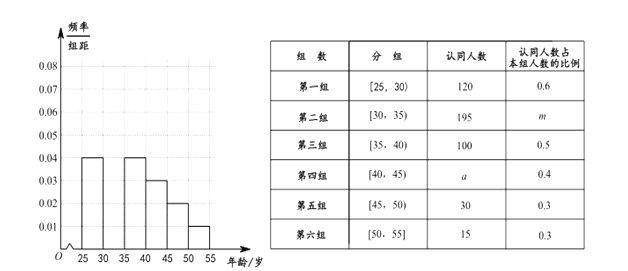
(Ⅰ)完成所給的頻率分布直方圖,并求![]() 的值;
的值;
(Ⅱ)如果從![]() 兩個年齡段中的“認同”人群中,按分層抽樣的方法抽取6人參與座談會,然后從這6人中隨機抽取2人作進一步調查,求這2人的年齡都在
兩個年齡段中的“認同”人群中,按分層抽樣的方法抽取6人參與座談會,然后從這6人中隨機抽取2人作進一步調查,求這2人的年齡都在![]() 內的概率 .
內的概率 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的奇數項成等差數列,偶數項成等比數列,且公差和公比都是2,若對滿足m+n≤5的任意正整數m,n,均有am+an=am+n成立. (I)求數列{an}的通項公式;
(II)若bn=  ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義區間[x1 , x2]長度為x2﹣x1(x2>x1),已知函數f(x)= ![]() (a∈R,a≠0)的定義域與值域都是[m,n],則區間[m,n]取最大長度時a的值是 .
(a∈R,a≠0)的定義域與值域都是[m,n],則區間[m,n]取最大長度時a的值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S﹣ABCD中,底面ABCD是直角梯形,側棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中點. (Ⅰ)求證:AM∥面SCD;
(Ⅱ)求面SCD與面SAB所成二面角的余弦值;
(Ⅲ)設點N是直線CD上的動點,MN與面SAB所成的角為θ,求sinθ的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (b∈R).若存在x∈[
(b∈R).若存在x∈[ ![]() ,2],使得f(x)+xf′(x)>0,則實數 b的取值范圍是( )
,2],使得f(x)+xf′(x)>0,則實數 b的取值范圍是( )
A.(﹣∞, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣∞,3)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一數學研究小組測量學校的一座教學樓AB的高度![]() 已知測角儀器距離地面的高度為h米,現有兩種測量方法:
已知測角儀器距離地面的高度為h米,現有兩種測量方法:
方法![]() 如圖
如圖![]() 用測角儀器,對準教學樓的頂部A,計算并記錄仰角
用測角儀器,對準教學樓的頂部A,計算并記錄仰角![]() ;
;![]() 后退a米,重復
后退a米,重復![]() 中的操作,計算并記錄仰角
中的操作,計算并記錄仰角![]() .
.
方法![]() 如圖
如圖![]() 用測角儀器,對準教學樓的頂部A底部B,測出教學樓的視角
用測角儀器,對準教學樓的頂部A底部B,測出教學樓的視角![]() ,測試點與教學樓的水平距離b米.
,測試點與教學樓的水平距離b米.
請你回答下列問題:
![]() 用數據
用數據![]() ,
,![]() ,a,h表示出教學樓AB的高度;
,a,h表示出教學樓AB的高度;
![]() 按照方法II,用數據
按照方法II,用數據![]() ,b,h表示出教學樓AB的高度.
,b,h表示出教學樓AB的高度.
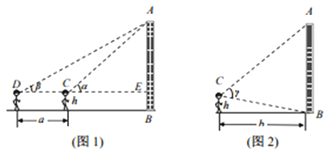
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com