考點:直線與圓錐曲線的綜合問題
專題:圓錐曲線中的最值與范圍問題
分析:(1)由橢圓的離心率e=
,得橢圓方程為
+=1,把點(1,
)代入,能求出橢圓的方程.
(2)設直線l為y=k(x-1),代入橢圓方程
+=1,得(3+4k
2)x
2-8k
2x+4k
2-12=0,由此利用根的判別式、韋達定理,結合已知條件能求出直線MN的方程.
解答:
解:(1)∵橢圓C:
+
=1(a>b>0)過點(1,
),
F
1、F
2分別為橢圓C的左、右兩個焦點,且離心率e=
,
∴
=,∴a=2c,∴b
2=a
2-c
2=3c
2,
∴橢圓方程為
+=1.…(2分)
把點(1,
)代入橢圓,得
+=1,解得c
2=1.
∴橢圓的方程為
+=1.…(4分)
(2)若直線l斜率不存在,
k1 +k2=0不合題意,
∴直線l的斜率存在.…(5分)
設直線l為y=k(x-1),代入橢圓方程
+=1,
得(3+4k
2)x
2-8k
2x+4k
2-12=0.…(7分)
依題意△=9k
2+9>0.
設M(x
1,y
1),N(x
2,y
2),則
x1+x2=,
x1x2=.…(8分)
∵k
1+k
2=-3,
∴k
1+k
2=
+=k(
+)
=k(2-
)
=k(2-
)=-3.…(10分)
整理,得k
2-2k-3=0,解得k=3或k=-1.
∴所求直線MN的方程為3x-y-3=0或x+y-1=0.…(12分)
點評:本題考查橢圓方程的求法,考查直線方程的求法,解題時要認真審題,注意韋達定理的靈活運用.



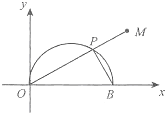 在直角坐標xoy中,以O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ=2cosθ,如圖,曲線C與x軸交于O,B兩點,P是曲線C在x軸上方圖象上任意一點,連結OP并延長至M,使PM=PB,當P變化時,求動點M的軌跡的長度.
在直角坐標xoy中,以O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ=2cosθ,如圖,曲線C與x軸交于O,B兩點,P是曲線C在x軸上方圖象上任意一點,連結OP并延長至M,使PM=PB,當P變化時,求動點M的軌跡的長度.