Question

【題目】已知，，對任意，有成立.

（1）求的通項公式；

（2）設，，是數列的前項和，求正整數，使得對任意，恒成立；

（3）設，是數列的前項和，若對任意均有恒成立，求的最小值.

Answer 1

【答案】（1） （2）或 （3）

【解析】

（1）由可得,結合平面向量的坐標運算可得到的關系式,再結合可證明數列是等比數列,進而可求出通項公式;

（2）將兩端同時除以,可得到,從而可證明數列是等差數列,即可求出的表達式,進而求得的通項公式,通過判斷其表達式特點,可求出滿足題意的正整數;

（3）由題得,,利用裂項相消求和法可求出,結合不等式的性質,可求出的最小值.

（1）由題可得,則,

當時,可得.

時,,則,即,

故數列是以2為首項,公比為2的等比數列,通項公式為.

（2）,等式兩端同時除以得:,即,

故是以為首項,公差為的等差數列,通項公式為,

則.

因為當，，當時,,所以當或時,取最大值,對任意，恒成立.

（3）由題意,,

則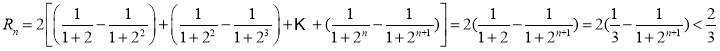,故.

所以的最小值為.