
【題目】如圖所示,已知焦點為![]() 的拋物線
的拋物線![]() 上有一動點
上有一動點![]() ,過點
,過點![]() 作拋物線的切線
作拋物線的切線![]() 交
交![]() 軸于點
軸于點![]() .
.
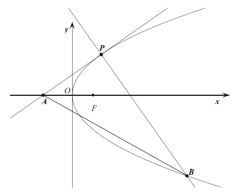
(1)判斷線段![]() 的中垂線是否過定點,若是求出定點坐標,若不是說明理由;
的中垂線是否過定點,若是求出定點坐標,若不是說明理由;
(2)過點![]() 作
作![]() 的垂線交拋物線于另一點
的垂線交拋物線于另一點![]() ,求
,求![]() 面積的最小值.
面積的最小值.
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() 為坐標原點,
為坐標原點, ![]() 是雙曲線上在第一象限內的點,直線
是雙曲線上在第一象限內的點,直線![]() 分別交雙曲線
分別交雙曲線![]() 左、右支于另一點
左、右支于另一點![]() ,
, ![]() ,且
,且![]() ,則雙曲線
,則雙曲線![]() 的離心率為( )
的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間用一臺包裝機包裝葡萄糖,每袋葡萄糖的重量是一個隨機變量,它服從正態分布.當機器工作正常時,每袋葡萄糖平均重量![]() 為0.5kg,標準差
為0.5kg,標準差![]() 為0.015kg.
為0.015kg.
(1)已知包裝每袋葡萄糖的成本為1元,若發現包裝好的葡萄糖重量異常,則需要將該袋葡萄糖進行重新包裝,假設重新包裝后的葡萄糖重量正常.若某袋葡萄糖的重量![]() 滿足
滿足![]() ,則認為該袋葡萄糖重量正常. 問:在機器工作正常的情況下,至少包裝多少袋葡萄糖才能使“至少有一袋包裝好的葡萄糖重量正常”的概率大于0.98?并求出相應成本的最小期望值.
,則認為該袋葡萄糖重量正常. 問:在機器工作正常的情況下,至少包裝多少袋葡萄糖才能使“至少有一袋包裝好的葡萄糖重量正常”的概率大于0.98?并求出相應成本的最小期望值.
(2)某日開工后, 為檢査該包裝機工作是否正常, 隨機地抽取它所包裝的葡萄糖9袋,若抽取的9袋葡萄糖稱得凈重(kg)為:0.496, 0.508, 0.524, 0.519, 0.495, 0.510, 0.522, 0.513, 0.512.用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,以
,以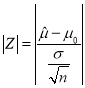 作為檢驗統計量,其中
作為檢驗統計量,其中![]() 為樣本總數,
為樣本總數,![]() 服從正態分布
服從正態分布![]() ,且
,且![]() .
.
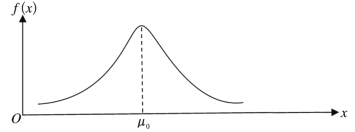
①若機器工作正常時, 每袋葡萄糖的重量服從的正態分布曲線如下圖所示,且經計算得上述樣本數據的標準差![]() 0.022.請在下圖(機器正常工作時的正態分布曲線)中,繪制出以該樣本作為估計得到的每袋葡萄糖所服從的正態分布曲線的草圖.
0.022.請在下圖(機器正常工作時的正態分布曲線)中,繪制出以該樣本作為估計得到的每袋葡萄糖所服從的正態分布曲線的草圖.
②若![]() ,就推斷該包裝機工作異常,這種推斷犯錯誤的概率不超過
,就推斷該包裝機工作異常,這種推斷犯錯誤的概率不超過![]() ,試以95%的可靠性估計該包裝機工作是否正常.
,試以95%的可靠性估計該包裝機工作是否正常.
附: 若隨機變量![]() 服從正態分布:
服從正態分布:![]() ,
,![]()
![]()
參考數據:![]() ;
;![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 是拋物線
是拋物線![]() 上的兩個不同的點,
上的兩個不同的點,![]() 是坐標原點.若直線
是坐標原點.若直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,則( ).
,則( ).
A.![]() B.以
B.以![]() 為直徑的圓的面積大于
為直徑的圓的面積大于![]()
C.直線![]() 過定點
過定點![]() D.點
D.點![]() 到直線
到直線![]() 的距離不大于2
的距離不大于2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等差數列![]() 中,已知
中,已知![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個補充在第(2)問中,并對其求解.
這三個條件中任選一個補充在第(2)問中,并對其求解.
(1)求數列![]() 的通項公式
的通項公式![]() ;
;
(2)若___________,求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙3人站到共有6級的臺階上,若每級臺階最多站2人,同一級臺階上的人不區分站的位置,則不同的站法總數是( )
A.90B.120C.210D.216
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,上頂點為M,過點M且斜率為
,上頂點為M,過點M且斜率為![]() 的直線與
的直線與![]() 交于另一點N,過原點的直線l與
交于另一點N,過原點的直線l與![]() 交于P,Q兩點
交于P,Q兩點
(1)求![]() 周長的最小值:
周長的最小值:
(2)是否存在這樣的直線,使得與直線![]() 平行的弦的中點都在該直線上?若存在,求出該直線的方程:若不存在,請說明理由.
平行的弦的中點都在該直線上?若存在,求出該直線的方程:若不存在,請說明理由.
(3)直線l與線段![]() 相交,且四邊形
相交,且四邊形![]() 的面積
的面積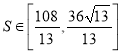 ,求直線l的斜率k的取值范圍.
,求直線l的斜率k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com