
【題目】設函數f(x)=aex﹣x﹣1,a∈R. (Ⅰ)當a=1時,求f(x)的單調區間;
(Ⅱ)當x∈(0,+∞)時,f(x)>0恒成立,求a的取值范圍;
(Ⅲ)求證:當x∈(0,+∞)時,ln ![]() >
> ![]() .
.
【答案】解:(Ⅰ)當a=1時,則f(x)=ex﹣x﹣1,f'(x)=ex﹣1; 令f'(x)=0,得x=0;
∴當x<0時,f'(x)<0,f(x)在(﹣∞,0)上單調遞減;
當x≥0時,f'(x)≥0,h(x)在(0,+∞)上單調遞增;
即a=1時,f(x)的單調減區間為(﹣∞,0),單調贈區間為[0,+∞);
(Ⅱ)∵ex>0;
∴f(x)>0恒成立,等價于 ![]() 恒成立;
恒成立;
設 ![]() ,x∈(0,+∞),
,x∈(0,+∞), ![]() ;
;
當x∈(0,+∞)時,g′(x)<0;
∴g(x)在(0,+∞)上單調遞減;
∴x∈(0,+∞)時,g(x)<g(0)=1;
∴a≥1;
∴a的取值范圍為[1,+∞);
(Ⅲ)證明:當x∈(0,+∞)時, ![]() 等價于ex﹣xex﹣1>0;
等價于ex﹣xex﹣1>0;
設h(x)=ex﹣xex﹣1,x∈(0,+∞), 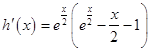 ;
;
由(Ⅱ)知,x∈(0,+∞)時,ex﹣x﹣1>0恒成立;
∴ ![]() ;
;
∴h′(x)>0;
∴h(x)在(0,+∞)上單調遞增;
∴x∈(0,+∞)時,h(x)>h(0)=0;
因此當x∈(0,+∞)時, ![]()
【解析】(Ⅰ)a=1時得出f(x),進而得到f′(x)=ex﹣1,這樣便可判斷導數符號,根據符號即可得出f(x)的單調區間;(Ⅱ)可以由f(x)>0恒成立得到 ![]() 恒成立,這樣設
恒成立,這樣設 ![]() ,求導,根據導數符號便可判斷g(x)在(0,+∞)上單調遞減,這便可得到g(x)<1,從而便可得出a的取值范圍;(Ⅲ)容易得到
,求導,根據導數符號便可判斷g(x)在(0,+∞)上單調遞減,這便可得到g(x)<1,從而便可得出a的取值范圍;(Ⅲ)容易得到 ![]() 等價于ex﹣xex﹣1>0,可設h(x)=ex﹣xex﹣1,求導數,并根據上面的f(x)>0可判斷出導數h′(x)>0,從而得到h(x)>h(0)=0,這樣即可得出要證明的結論.
等價于ex﹣xex﹣1>0,可設h(x)=ex﹣xex﹣1,求導數,并根據上面的f(x)>0可判斷出導數h′(x)>0,從而得到h(x)>h(0)=0,這樣即可得出要證明的結論.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,an+1=1﹣ ![]() ,其中n∈N* .
,其中n∈N* .
(1)設bn= ![]() ,求證:數列{bn}是等差數列,并求出{an}的通項公式;
,求證:數列{bn}是等差數列,并求出{an}的通項公式;
(2)設cn= ![]() ,數列{cncn+2}的前n項和為Tn , 求證:Tn<3.
,數列{cncn+2}的前n項和為Tn , 求證:Tn<3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等比數列,滿足a2=6,a3=﹣18,數列{bn}滿足b1=2,且{2bn+an}是公差為2的等差數列.
(Ⅰ)求數列{an}和{bn}的通項公式;
(Ⅱ)求數列{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)在R上是增函數,則下列說法正確的是( )
A.y=﹣f(x)在R上是減函數
B.y= ![]() 在R上是減函數
在R上是減函數
C.y=[f(x)]2在R上是增函數
D.y=af(x)(a為實數)在R上是增函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為D={x|x≠0},且滿足對于任意x1 , x2∈D,有f(x1x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判斷f(x)的奇偶性并證明你的結論;
(3)如果f(4)=1,f(x﹣1)<2,且f(x)在(0,+∞)上是增函數,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列各組函數是否為相等函數:
⑴f(x)=f(x)= ![]() ,g(x)=x﹣5;
,g(x)=x﹣5;
⑵f(x)=2x+1(x∈Z),g(x)=2x+1(x∈R);
⑶f(x)=|x+1|,g(x)= ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(1+x)﹣x+ ![]() x2(k≥0). (Ⅰ)當k=2時,求曲線y=f(x)在點(1,f(1))處的切線方程;
x2(k≥0). (Ⅰ)當k=2時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(Ⅱ)求f(x)的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x1、x2是一元二次方程4kx2﹣4kx+k+1=0的兩個實數根.
(1)是否存在實數k,(2x1﹣x2)(x1﹣2x2)=﹣ ![]() 成立?若存在,求出k的值;若不存在,請說明理由.
成立?若存在,求出k的值;若不存在,請說明理由.
(2)求使 ![]() +
+ ![]() ﹣2的值為整數的實數k的整數值.
﹣2的值為整數的實數k的整數值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區2007年至2013年農村居民家庭人均純收入y(單位:千元)的數據如表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y關于t的線性回歸方程;
(Ⅱ)利用(Ⅰ)中的回歸方程,分析2007年至2013年該地區農村居民家庭人均純收入的變化情況,并預測該地區2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘估計公式分別為: ![]() =
= 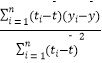 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com