
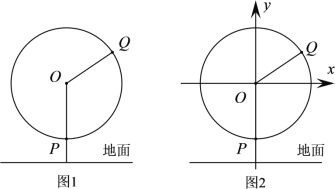
【題目】隨著我國綜合國力的不斷增強,不少綜合性娛樂場所都引進了“摩天輪”這一娛樂設施.(如圖1)有一半徑為40m的摩天輪,軸心![]() 距地面50m,摩天輪按逆時針方向做勻速旋轉,轉一周需要3min.點
距地面50m,摩天輪按逆時針方向做勻速旋轉,轉一周需要3min.點![]() 與點
與點![]() 都在摩天輪上,且點
都在摩天輪上,且點![]() 相對于點
相對于點![]() 落后1min,當點
落后1min,當點![]() 在摩天輪的最低點處時開始計時,以軸心
在摩天輪的最低點處時開始計時,以軸心![]() 為坐標原點,平行于地面且在摩天輪所在平面內的直線為
為坐標原點,平行于地面且在摩天輪所在平面內的直線為![]() 軸,建立圖2所示的平面直角坐標系.
軸,建立圖2所示的平面直角坐標系.

(1)若![]() ,求點
,求點![]() 的縱坐標關于時間
的縱坐標關于時間![]() 的函數關系式
的函數關系式![]() ;
;
(2)若![]() ,求點
,求點![]() 距離地面的高度關于時間
距離地面的高度關于時間![]() 的函數關系式
的函數關系式![]() ,并求
,并求![]() 時,點
時,點![]() 離地面的高度(結果精確到0.1,計算所用數據:
離地面的高度(結果精確到0.1,計算所用數據:![]() )
)
(3)若![]() ,當
,當![]() ,
,![]() 兩點距離地面的高度差不超過
兩點距離地面的高度差不超過![]() 時,求時間
時,求時間![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;40.2m;(3)
;40.2m;(3)![]() .
.
【解析】
(1)由題可知,當![]() 時,以
時,以![]() 為終邊的角與
為終邊的角與![]() 的角終邊重合,且
的角終邊重合,且![]() 轉動的角速度為
轉動的角速度為![]() ,即可得出
,即可得出![]() 時
時![]() 終邊所在的角度為
終邊所在的角度為![]() ,從而得出
,從而得出![]() 的關系式;
的關系式;
(2)由于軸心![]() 距地面50m,得出
距地面50m,得出![]() ,即可得出點
,即可得出點![]() 距離地面的高度關于時間
距離地面的高度關于時間![]() 的函數關系式
的函數關系式![]() ,從而可求出
,從而可求出![]() ,即得出點
,即得出點![]() 離地面的高度;
離地面的高度;
(3)設Q點離地面的高度與時間的函數關系式為![]() ,則
,則![]() ,
,![]() ,進而得出
,進而得出![]() ,
,![]() 兩點距離地面的高度差不超過
兩點距離地面的高度差不超過![]() 的不等式,即
的不等式,即![]()
![]() ,解不等式從而求出
,解不等式從而求出![]() 的取值范圍.
的取值范圍.
解:(1)當![]() 時,以
時,以![]() 為終邊的角與
為終邊的角與![]() 的角終邊重合,
的角終邊重合,
且![]() 轉動的角速度為
轉動的角速度為![]() ,
,
所以![]() 時,
時,![]() 終邊所在的角度為
終邊所在的角度為![]() ,
,
所以![]() .
.
(2)由題知,點![]() 距離地面的高度關于時間
距離地面的高度關于時間![]() 的函數關系式
的函數關系式![]() ,
,
則![]() ,
,
![]() ,
,
當![]() 時,
時,
則![]()
![]()
![]()
![]()
![]() .
.
(3)設Q點離地面的高度與時間的函數關系式為![]() ,
,
則![]() ,
,![]() ,
,
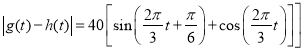
![]() ,
,
所以![]() ,即
,即![]() ,
,
因為![]() ,所以
,所以![]() ,
,
因為![]() 在
在![]() 上遞減,在
上遞減,在![]() 遞增,
遞增,
又因為![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
或![]() ,即
,即![]() ,
,
所以![]() 時P,Q兩點的高度差不超過
時P,Q兩點的高度差不超過![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點到準線的距離為
的焦點到準線的距離為![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,過這兩點分別作拋物線
兩點,過這兩點分別作拋物線![]() 的切線,且這兩條切線相交于點
的切線,且這兩條切線相交于點![]() .
.
(1)若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 的值;
的值;
(2)設線段![]() 的中點為
的中點為![]() ,過
,過![]() 的直線
的直線![]() 與線段
與線段![]() 為直徑的圓相切,切點為
為直徑的圓相切,切點為![]() ,且直線
,且直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到焦點
到焦點![]() 的距離
的距離![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)過點![]() 引圓
引圓![]() 的兩條切線
的兩條切線![]() ,切線
,切線![]() 與拋物線
與拋物線![]() 的另一交點分別為
的另一交點分別為![]() ,線段
,線段![]() 中點的橫坐標記為
中點的橫坐標記為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生為了測試煤氣灶燒水如何節省煤氣的問題設計了一個實驗,并獲得了煤氣開關旋鈕旋轉的弧度數x與燒開一壺水所用時間y的一組數據,且作了一定的數據處理(如表),得到了散點圖(如圖).
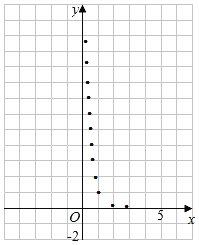

表中![]() ,
,![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作燒水時間y關于開關旋鈕旋轉的弧度數x的回歸方程類型?(不必說明理由)
哪一個更適宜作燒水時間y關于開關旋鈕旋轉的弧度數x的回歸方程類型?(不必說明理由)
(2)根據判斷結果和表中數據,建立y關于x的回歸方程;
(3)若旋轉的弧度數x與單位時間內煤氣輸出量t成正比,那么x為多少時,燒開一壺水最省煤氣?
附:對于一組數據![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為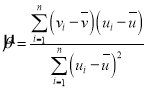 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】惠州市某商店銷售某海鮮,經理統計了春節前后50天該海鮮的日需求量![]() (
(![]() ,單位:公斤),其頻率分布直方圖如下圖所示.該海鮮每天進貨1次,每銷售1公斤可獲利40元;若供大于求,剩余的海鮮削價處理,削價處理的海鮮每公斤虧損10元;若供不應求,可從其它商店調撥,調撥的海鮮銷售1公斤可獲利30元.假設商店該海鮮每天的進貨量為14公斤,商店銷售該海鮮的日利潤為
,單位:公斤),其頻率分布直方圖如下圖所示.該海鮮每天進貨1次,每銷售1公斤可獲利40元;若供大于求,剩余的海鮮削價處理,削價處理的海鮮每公斤虧損10元;若供不應求,可從其它商店調撥,調撥的海鮮銷售1公斤可獲利30元.假設商店該海鮮每天的進貨量為14公斤,商店銷售該海鮮的日利潤為![]() 元.
元.
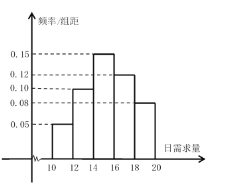
(1)求商店日利潤![]() 關于日需求量
關于日需求量![]() 的函數表達式.
的函數表達式.
(2)根據頻率分布直方圖,
①估計這50天此商店該海鮮日需求量的平均數.
②假設用事件發生的頻率估計概率,請估計日利潤不少于620元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com