
【題目】已知函數f(x)=a﹣![]() (a∈R)
(a∈R)
(1)如果函數f(x)為奇函數,求實數a的值;
(2)證明:對任意的實數a,函數f(x)在(﹣∞,+∞)上是增函數.
科目:高中數學 來源: 題型:
【題目】如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是線段EF的中點.
,AF=1,M是線段EF的中點. 
(Ⅰ)求證AM∥平面BDE;
(Ⅱ)求二面角A﹣DF﹣B的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設圓x2+y2=12與拋物線x2=4y相交于A,B兩點,F為拋物線的焦點,若過點F且斜率為1的直線l與拋物線和圓交于四個不同的點,從左至右依次為P1 , P2 , P3 , P4 , 則|P1P2|+|P3P4|的值 , 若直線m與拋物線相交于M,N兩點,且與圓相切,切點D在劣弧 ![]() 上,則|MF|+|NF|的取值范圍是 .
上,則|MF|+|NF|的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() .
.
(1)求函數f(x)的最小正周期和單調減區間;
(2)已知△ABC的三個內角A,B,C的對邊分別為a,b,c,其中a=7,若銳角A滿足 ![]() ,且
,且 ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() +
+ ![]() =1(a>b>0)的左右焦點F1 , F2其離心率為e=
=1(a>b>0)的左右焦點F1 , F2其離心率為e= ![]() ,點P為橢圓上的一個動點,△PF1F2內切圓面積的最大值為
,點P為橢圓上的一個動點,△PF1F2內切圓面積的最大值為 ![]() .
.
(1)求a,b的值
(2)若A、B、C、D是橢圓上不重合的四個點,且滿足 ![]() ,
, ![]() =0,求|
=0,求| ![]() |+|
|+| ![]() |的取值范圍.
|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
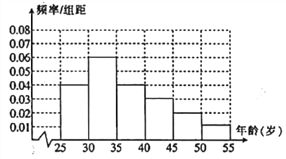
【題目】某高校進行社會實踐,對![]() 歲的人群隨機抽取 1000 人進行了一次是否開通“微博”的調查,開通“微博”的為“時尚族”,否則稱為“非時尚族”.通過調查得到到各年齡段人數的頻率分布直方圖如圖所示,其中在
歲的人群隨機抽取 1000 人進行了一次是否開通“微博”的調查,開通“微博”的為“時尚族”,否則稱為“非時尚族”.通過調查得到到各年齡段人數的頻率分布直方圖如圖所示,其中在![]() 歲,
歲, ![]() 歲年齡段人數中,“時尚族”人數分別占本組人數的
歲年齡段人數中,“時尚族”人數分別占本組人數的![]() 、
、![]() .
.
(1)求![]() 歲與
歲與![]() 歲年齡段“時尚族”的人數;
歲年齡段“時尚族”的人數;
(2)從![]() 歲和
歲和![]() 歲年齡段的“時尚族”中,采用分層抽樣法抽取6人參加網絡時尚達人大賽,其中兩人作為領隊.求領隊的兩人年齡都在
歲年齡段的“時尚族”中,采用分層抽樣法抽取6人參加網絡時尚達人大賽,其中兩人作為領隊.求領隊的兩人年齡都在![]() 歲內的概率。
歲內的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)是定義在(﹣∞,+∞)上的偶函數,x1 , x2∈[0,+∞)(x1≠x2),有 ![]() ,則( )
,則( )
A.f(3)<f(1)<f(﹣2)
B.f(1)<f(﹣1)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(﹣2)<f(1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com