Question

【題目】如圖，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB= ，AF=1，M是線段EF的中點．
（Ⅰ）求證AM∥平面BDE；
（Ⅱ）求二面角A﹣DF﹣B的大小．

Answer 1

【答案】解：方法一（Ⅰ）記AC與BD的交點為O，連接OE，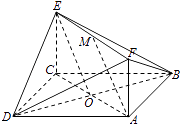

∵O、M分別是AC、EF的中點，ACEF是矩形，
∴四邊形AOEM是平行四邊形，
∴AM∥OE
∵OE平面BDE，AM平面BDE，
∴AM∥平面BDE
（Ⅱ）在平面AFD中過A作AS⊥DF于S，連接BS，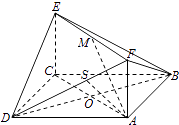

∵AB⊥AF，AB⊥AD，AD∩AF=A，
∴AB⊥平面ADF，
∴AS是BS在平面ADF上的射影，
由三垂線定理得BS⊥DF
∴∠BSA是二面角A﹣DF﹣B的平面角
在Rt△ASB中，AS= = ，AB= ，
∴ ，
∴二面角A﹣DF﹣B的大小為60°
方法二
（Ⅰ）建立如圖所示的空間直角坐標系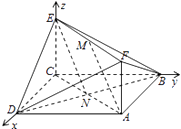

設AC∩BD=N，連接NE，
則點N、E的坐標分別是（ 、（0，0，1），
∴ =（ ，
又點A、M的坐標分別是
（ ）、（
∴ =（
∴ = 且NE與AM不共線，
∴NE∥AM
又∵NE平面BDE，AM平面BDE，
∴AM∥平面BDF
（Ⅱ）∵AF⊥AB，AB⊥AD，AF∩AD=A，
∴AB⊥平面ADF
∴ 為平面DAF的法向量
∵ =（ =0，
∴ =（ =0得 ， ∴NE為平面BDF的法向量
∴cos＜ ＞=
∴ 的夾角是60°
即所求二面角A﹣DF﹣B的大小是60°
【解析】（Ⅰ）要證AM∥平面BDE，直線證明直線AM平行平面BDE內的直線OE即可，也可以利用空間直角坐標系，求出向量 ，在平面BDE內求出向量 ，證明二者共線，說明AM∥平面BDE，（Ⅱ）在平面AFD中過A作AS⊥DF于S，連接BS，說明∠BSA是二面角A﹣DF﹣B的平面角，然后求二面角A﹣DF﹣B的大小；也可以建立空間直角坐標系，求出 ， 說明 是平面DFB的法向量，求出平面DAF的法向量 ，然后利用數量積求解即可．
【考點精析】本題主要考查了直線與平面平行的判定的相關知識點，需要掌握平面外一條直線與此平面內的一條直線平行，則該直線與此平面平行；簡記為：線線平行，則線面平行才能正確解答此題．