
【題目】隨著手機的發展,“微信”越來越成為人們交流的一種方式.某機構對“使用微信交流”的態度進行調查,隨機抽取了50人,他們年齡的頻數分布及對“使用微信交流”贊成人數如下表.
年齡(單位:歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年齡45歲為分界點”,由以上統計數據完成下面![]() 列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(2)若從年齡在[55,65)的被調查人中隨機選取2人進行追蹤調查,求2人中至少有1人不贊成“使用微信交流”的概率.
參考數據如下:

![]()
【答案】(1)列聯表見解析;有![]() %的把握認為“使用微信交流”的態度與人的年齡有關;
%的把握認為“使用微信交流”的態度與人的年齡有關;
(2)![]() .
.
【解析】
試題分析:(1)很容易完成列聯表;代入公式求得![]() ,由給定的值可得結論;(2)利用古典概型可得基本事件共
,由給定的值可得結論;(2)利用古典概型可得基本事件共![]() 個,不滿足題意的基本事件共
個,不滿足題意的基本事件共![]() 個,利用對立事件可求得
個,利用對立事件可求得![]() 人中至少有
人中至少有![]() 人不贊成“使用微信交流”的概率.
人不贊成“使用微信交流”的概率.
試題解析: (1)![]() 列聯表:
列聯表:
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | 10 | 27 | 37 |
不贊成 | 10 | 3 | 13 |
合計 | 20 | 30 | 50 |
∴![]() .
.
∴有99%的把握認為“使用微信交流”的態度與人的年齡有關.
(2)設[55,65)中不贊成“使用微信交流”的人為![]() ,贊成“使用微信交流”的人為
,贊成“使用微信交流”的人為![]() ,則從5人中選取2人有:
,則從5人中選取2人有:![]() 共10個結果,其中兩人都贊成“使用微信交流”的有1個結果,所以2人中至少有1人不贊成“使用微信交流”的概率為
共10個結果,其中兩人都贊成“使用微信交流”的有1個結果,所以2人中至少有1人不贊成“使用微信交流”的概率為![]() .
.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
【題目】如圖,一個側棱長為![]() 的直三棱柱
的直三棱柱![]() 容器中盛有液體(不計容器厚度).若液面恰好分別過棱
容器中盛有液體(不計容器厚度).若液面恰好分別過棱![]() 中點
中點![]() .
.
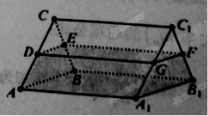
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當底面![]() 水平放置時,求液面的高.
水平放置時,求液面的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的公差不為零,首項a1=1,a2是a1和a5的等比中項,則數列的前10項之和是( )
A. 90 B. 100 C. 145 D. 190
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在建立兩個變量Y與x的回歸模型中,分別選擇了4個不同模型,它們的相關指數R2如下,其中擬合得最好的模型是 ( )
A. 模型1的相關指數R2為0.98 B. 模型2的相關指數R2為0.80
C. 模型3的相關指數R2為0.50 D. 模型4的相關指數R2為0.25
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(1,0,2),B(1,-3,1),點M在z軸上且到A、B兩點的距離相等,則點M的坐標為
A. (-3,0,0) B. (0,-3,0) C. (0,0,3) D. (0,0,-3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于①“一定發生的”,②“很可能發生的”,③“可能發生的”,④“不可能發生的”,⑤“不太可能發生的”這5種生活現象,發生的概率由小到大排列為(填序號)_________________。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點
的中心在原點![]() ,焦點在
,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,右焦點到右頂點的距離為
,右焦點到右頂點的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)是否存在與橢圓![]() 交于
交于![]() 兩點的直線
兩點的直線![]() :
:![]() ,使得
,使得![]() 成立?若存在,求出實數
成立?若存在,求出實數![]() 的取值范圍,若不存在,請說明理由.
的取值范圍,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com