Question

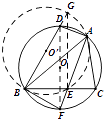
【題目】如圖所示，△ABC內接于圓O，D是 的中點，∠BAC的平分線分別交BC和圓O于點E，F．

（1）求證：BF是△ABE外接圓的切線；
（2）若AB=3，AC=2，求DB2﹣DA2的值．

Answer 1

【答案】
（1）解：設△ABE外接圓的圓心為O′，連結BO′并延長交圓O′于G點，連結GE，

則∠BEG=90°，∠BAE=∠BGE．

因為AF平分∠BAC，

所以 ，

所以∠FBE=∠BAE，

所以∠FBG=∠FBE+∠EBG=∠BGE+∠EBG=180°﹣∠BEG=90°，

所以O′B⊥BF，

所以BF是△ABE外接圓的切線

（2）解：連接DF，則DF⊥BC，

所以DF是圓O的直徑，

因為BD2+BF2=DF2，DA2+AF2=DF2，

所以BD2﹣DA2=AF2﹣BF2．

因為AF平分∠BAC，

所以△ABF∽△AEC，

所以 ，

所以ABAC=AEAF=（AF﹣EF）AF，

因為∠FBE=∠BAE，

所以△FBE∽△FAB，從而BF2=FEFA，

所以AB﹣AC=AF2﹣BF2，

所以BD2﹣DA2=ABAC=6

【解析】（1）設△ABE外接圓的圓心為O′，連結BO′并延長交圓O′于G點，連結GE，則∠BEG=90°，∠BAE=∠BGE，可證∠FBE=∠BAE，進而證明∠FBG=90°，即可得證BF是△ABE外接圓的切線．（2）連接DF，則DF⊥BC，由勾股定理可得BD2﹣DA2=AF2﹣BF2 ， 利用相似三角形的性質可得ABAC=AEAF=（AF﹣EF）AF，由△FBE∽△FAB，從而BF2=FEFA，得AB﹣AC=AF2﹣BF2 ， 進而可求BD2﹣DA2=ABAC=6．