(本題滿分12分)過點
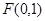
作直線
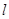
與拋物線
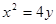
相交于兩點
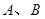
,圓
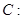
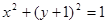
(1)若拋物線在點
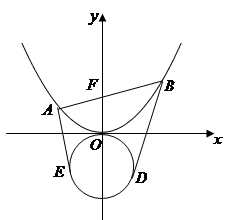
處的切線恰好與圓
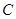
相切,求直線
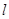
的方程;
(2)過點
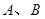
分別作圓
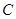
的切線
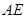
,
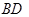
試求
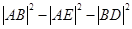
的取值范圍.
(I)
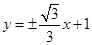
. (Ⅱ)
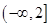
.
試題分析:(I)設
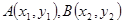
由
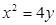
,得
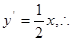
過點
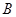
的切線方程為:
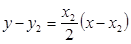
,即
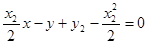
(3分)
由已知:
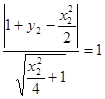
,又
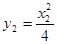
, (5分)
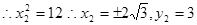
,即點
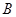
坐標為

, (6分)
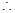
直線
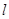
的方程為:
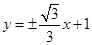
. (7分)
(Ⅱ)由已知,直線
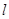
的斜率存在,則設直線
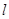
的方程為:
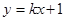
,(8分)
聯(lián)立
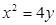
,得


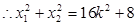
(9分)
解法二:
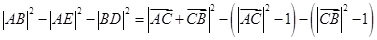
(12分)
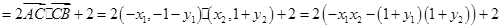
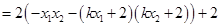
(13分)
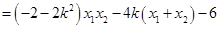

(15分)
解法三:
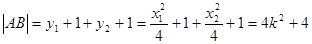
,

同理,
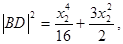
(13分)
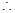

故
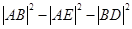
的取值范圍是
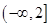
. (15分)
點評:容易題,曲線關系問題,往往通過聯(lián)立方程組,得到一元二次方程,運用韋達定理。本題(2)解法較多,但都涉及到整體代換,簡化證明過程,值得學習。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分10分)
已知一條曲線上的點到定點
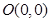
的距離是到定點

距離的二倍,求這條曲線的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設點
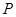
是以
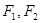
為左、右焦點的雙曲線
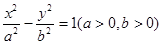
左支上一點,且滿足
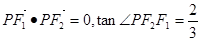
,則此雙曲線的離心率為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
過橢圓
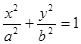
的左焦點作直線交橢圓于
、
兩點,若存在直線使坐標原點
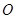
恰好在以
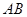
為直徑的圓上,則橢圓的離心率取值范圍是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在橢圓
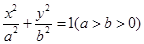
中,
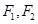
分別是其左右焦點,若
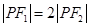
,則該橢圓離心率的取值范圍是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若拋物線
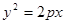
的焦點與雙曲線
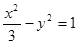
的左焦點重合,則實數(shù)
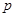
=
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知橢圓
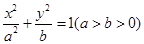
的左、右焦點分別為
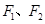
,離心率
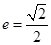
,
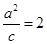
.
(I)求橢圓的標準方程;
(II)過點
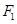
的直線
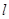
與該橢圓交于
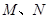
兩點,且
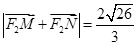
,求直線
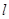
的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知拋物線
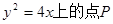
到拋物線的準線距離為d
1,到直線
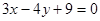
的距離為d
2,則d
1+d
2的最小值是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
雙曲線
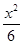
-
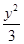
=1的漸近線與圓(x-3)
2+y
2=r
2(r>0)相切,則r=( )
A.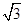 | B.2 | C.3 | D.6 |
查看答案和解析>>

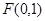 作直線
作直線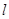 與拋物線
與拋物線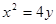 相交于兩點
相交于兩點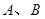 ,圓
,圓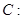
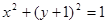

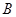 處的切線恰好與圓
處的切線恰好與圓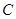 相切,求直線
相切,求直線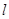 的方程;
的方程;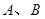 分別作圓
分別作圓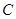 的切線
的切線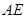 ,
,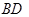 試求
試求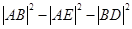 的取值范圍.
的取值范圍.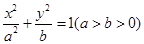 的左、右焦點分別為
的左、右焦點分別為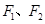 ,離心率
,離心率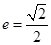 ,
, 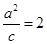 .
.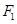 的直線
的直線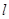 與該橢圓交于
與該橢圓交于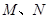 兩點,且
兩點,且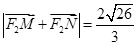 ,求直線
,求直線 的方程.
的方程.