
【題目】已知函數![]()
![]() 的圖像兩相鄰對稱軸之間的距離是
的圖像兩相鄰對稱軸之間的距離是![]() ,若將
,若將![]() 的圖像先向右平移
的圖像先向右平移![]() 個單位,再向上平移
個單位,再向上平移![]() 個單位,所得函數
個單位,所得函數![]() 為奇函數.
為奇函數.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的對稱軸及單調區間;
的對稱軸及單調區間;
(3)若對任意![]() ,
,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:高中數學 來源: 題型:
【題目】已知在一次射擊預選賽中,甲、乙兩人各射擊![]() 次,兩人成績的條形統計圖如圖所示,則下列四個選項中判斷不正確的是( )
次,兩人成績的條形統計圖如圖所示,則下列四個選項中判斷不正確的是( )

A. 甲的成績的平均數小于乙的成績的平均數
B. 甲的成績的中位數小于乙的成績的中位數
C. 甲的成績的方差大于乙的成績的方差
D. 甲的成績的極差小于乙的成績的極差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)估計該企業的職工對該部門評分不低于80的概率;
(3)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知過原點O的直線與函數![]() 的圖象交于A,B兩點,分別過A,B作y軸的平行線與函數
的圖象交于A,B兩點,分別過A,B作y軸的平行線與函數![]() 圖象交于C,D兩點,若
圖象交于C,D兩點,若![]() 軸,則四邊形ABCD的面積為_____.
軸,則四邊形ABCD的面積為_____.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高二年級一個學習興趣小組進行社會實踐活動,決定對某“著名品牌”![]() 系列進行市場銷售量調研,通過對該品牌的
系列進行市場銷售量調研,通過對該品牌的![]() 系列一個階段的調研得知,發現
系列一個階段的調研得知,發現![]() 系列每日的銷售量
系列每日的銷售量![]() (單位:千克)與銷售價格
(單位:千克)與銷售價格![]() (元/千克)近似滿足關系式
(元/千克)近似滿足關系式![]() ,其中
,其中![]() ,
,![]() 為常數.已知銷售價格為6元/千克時,每日可售出
為常數.已知銷售價格為6元/千克時,每日可售出![]() 系列15千克.
系列15千克.
(1)求函數![]() 的解析式;
的解析式;
(2)若![]() 系列的成本為4元/千克,試確定銷售價格
系列的成本為4元/千克,試確定銷售價格![]() 的值,使該商場每日銷售
的值,使該商場每日銷售![]() 系列所獲得的利潤最大.
系列所獲得的利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱臺ABCD﹣A1B1C1D1中,AA1⊥底面ABCD,四邊形ABCD為菱形,∠BAD=120°,AB=AA1=2A1B1=2. (Ⅰ)若M為CD中點,求證:AM⊥平面AA1B1B;
(Ⅱ)求直線DD1與平面A1BD所成角的正弦值.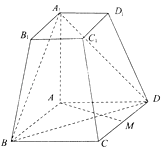
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表中提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量![]() (噸)與相應的生產能耗
(噸)與相應的生產能耗![]() (噸標準煤)的四組對應數據.
(噸標準煤)的四組對應數據.
| 6 | 8 | 10 | 12 |
| 2.5 | 3 | 4 | 4.5 |
(1)根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)已知該廠技改前100噸甲產品的生產能耗為45噸標準煤,試根據(1)中的線性回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣aex﹣e2x(a∈R,e是自然對數的底數). (Ⅰ)若f(x)≤0對任意x∈R恒成立,求實數a的取值范圍;
(Ⅱ)若方程x﹣aex=0有兩個不同的實數解x1 , x2 , 求證:x1+x2>2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+a|+|2x+1|,a∈R.
(1)當a=1時,求不等式f(x)≤1的解集;
(2)設關于x的不等式f(x)≤-2x+1的解集為P,且![]() P,求a的取值范圍.
P,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com