
【題目】選修4-4:坐標系與參數方程
已知曲線![]()
(1)化![]() 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)若![]() 上的點P對應的參數為
上的點P對應的參數為![]() ,Q為
,Q為![]() 上的動點,求PQ的中點M到直線
上的動點,求PQ的中點M到直線![]()
【答案】(1)C1:(x+4)2+(y-3)2=1,C2:![]() .C1為圓心是(-4,3),半徑是1的圓.C2為中心是坐標原點,焦點在x軸上,長半軸長是8,短半軸長是3的橢圓.
.C1為圓心是(-4,3),半徑是1的圓.C2為中心是坐標原點,焦點在x軸上,長半軸長是8,短半軸長是3的橢圓.
(2)![]() .
.
【解析】
試題分析:(1)利用三角函數中的平方關系![]() 消去參數可得普通方程;(2)用參數方程寫出Q點坐標,求出中點M的坐標,把直線
消去參數可得普通方程;(2)用參數方程寫出Q點坐標,求出中點M的坐標,把直線![]() 方程化為普通方程,由點到直線距離公式求出
方程化為普通方程,由點到直線距離公式求出![]() ,由三角函數的性質可得最值.
,由三角函數的性質可得最值.
試題解析:(1)C1:(x+4)2+(y-3)2=1,C2:![]() .
.
C1為圓心是(-4,3),半徑是1的圓.
C2為中心是坐標原點,焦點在x軸上,長半軸長是8,短半軸長是3的橢圓.
(2)當t=![]() 時,P(-4,4),Q(8cos
時,P(-4,4),Q(8cos![]() ,3sin
,3sin![]() ),故M
),故M![]() .
.
C3為直線x-2y-7=0,M到C3的距離d=![]() |4cos
|4cos![]() -3sin
-3sin![]() -13|.
-13|.
從而當cos![]() =
=![]() ,sin
,sin![]() =-
=-![]() 時,d取得最小值
時,d取得最小值![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知直線![]() (
(![]() ).
).
(1)證明:直線![]() 過定點;
過定點;
(2)若直線不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 軸負半軸于
軸負半軸于![]() ,交
,交![]() 軸正半軸于
軸正半軸于![]() ,△
,△![]() 的面積為
的面積為![]() (
(![]() 為坐標原點),求
為坐標原點),求![]() 的最小值,并求此時直線
的最小值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
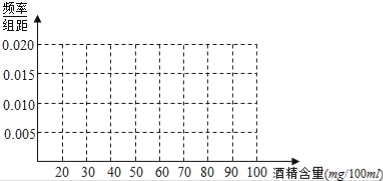
【題目】《中華人民共和國道路交通安全法》規定:車輛駕駛員血液酒精濃度在20~80mg/100ml(不含80)之間,屬于酒后駕車;在80mg/100ml(含80)以上時,屬于醉酒駕車.某市公安局交通管理部門在某路段的一次攔查行動中,依法檢查了300輛機動車,查處酒后駕車和醉酒駕車的駕駛員共20人,檢測結果如表:
酒精含量(mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70)[] | [70,80) | [80,90) | [90,100] |
人數 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(Ⅰ)繪制出檢測數據的頻率分布直方圖(在圖中用實線畫出矩形框即可);
(Ⅱ)求檢測數據中醉酒駕駛的頻率,并估計檢測數據中酒精含量的眾數、平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把離心率![]() 的雙曲線
的雙曲線![]() 稱為黃金雙曲線.給出以下幾個說法:
稱為黃金雙曲線.給出以下幾個說法:
①雙曲線![]() 是黃金雙曲線;
是黃金雙曲線;
②若雙曲線上一點![]() 到兩條漸近線的距離積等于
到兩條漸近線的距離積等于![]() ,則該雙曲線是黃金雙曲線;
,則該雙曲線是黃金雙曲線;
③若![]() 為左右焦點,
為左右焦點,![]() 為左右頂點,
為左右頂點,![]() 且
且![]() ,則該雙曲線是黃金雙曲線;
,則該雙曲線是黃金雙曲線;
④.若直線![]() 經過右焦點
經過右焦點![]() 交雙曲線于
交雙曲線于![]() 兩點,且
兩點,且![]() ,
,![]() ,則該雙曲線是黃金雙曲線;
,則該雙曲線是黃金雙曲線;
其中正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①所示,四邊形![]() 為等腰梯形,
為等腰梯形,![]() ,且
,且![]() 于點
于點![]() 為
為![]() 的中點.將
的中點.將![]() 沿著
沿著![]() 折起至
折起至![]() 的位置,得到如圖②所示的四棱錐
的位置,得到如圖②所示的四棱錐![]() .
.
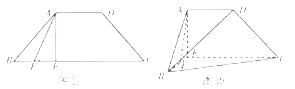
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各式:
(1)![]() ;
;
(2)已知![]() ,則
,則![]() ;
;
(3)函數![]() 的圖象與函數
的圖象與函數![]() 的圖象關于y軸對稱;
的圖象關于y軸對稱;
(4)函數![]() 的定義域是R,則m的取值范圍是
的定義域是R,則m的取值范圍是![]() ;
;
(5)函數![]() 的遞增區間為
的遞增區間為![]() .
.
正確的有______________________.(把你認為正確的序號全部寫上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com