
【題目】若對于x>0, ![]() ≤a恒成立,則a的取值范圍是
≤a恒成立,則a的取值范圍是
【答案】[ ![]() ,+∞)
,+∞)
【解析】解:∵對于x>0, ![]() ≤a恒成立,故函數f(x)=
≤a恒成立,故函數f(x)= ![]() 的最大值小于等于a,
的最大值小于等于a,
∵f′(x)=  ,
,
故當x<﹣1時,f′(x)<0,函數f(x)為減函數,且恒為負,
當﹣1<x≤1時,f′(x)≥0,函數f(x)為增函數,且恒為正,
當x>1時,f′(x)<0,函數f(x)為減函數,且恒為正,
即x=1時,函數有最大值 ![]()
故a的取值范圍是:[ ![]() ,+∞),
,+∞),
所以答案是:[ ![]() ,+∞).
,+∞).
【考點精析】關于本題考查的命題的真假判斷與應用和函數的最大(小)值與導數,需要了解兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.
比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐E﹣ABCD中,底面ABCD為矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F為CE的中點,求證: 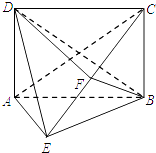
(1)AE∥平面BDF;
(2)平面BDF⊥平面ACE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線
軸的正半軸為極軸,取相同的長度單位建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值;
的距離的最大值;
(2)若曲線![]() 上的所有點都在直線
上的所有點都在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知y= ![]() x3+bx2+(b+2)x+3是R上的單調增函數,則b的取值是( )
x3+bx2+(b+2)x+3是R上的單調增函數,則b的取值是( )
A.b<﹣1或b>2
B.b≤﹣2或b≥2
C.﹣1<b<2
D.﹣1≤b≤2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一條對稱軸為
的一條對稱軸為![]() ,且最高點的縱坐標是
,且最高點的縱坐標是![]() .
.
(1)求![]() 的最小值及此時函數
的最小值及此時函數![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情況下,設![]() ,求函數
,求函數![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com